Гіпергеометричний закон розподілу ймовірностей. Числові характеристики
Гіпергеометричний закон розподілу ймовірностей настільки важкий при першому ознайомленні, що краще за все його пояснювати на конкретному прикладі.
Нехай задано деяку множину однотипних елементів, число яких дорівнює N; з них K елементів мають, наприклад, ознаку А (колір, стандартність, наповнення), а решта N-K елементів — ознаку В. З цієї множини навмання беруть nелементів. Випадкова величина X – число елементів з ознакою А, що трапляється серед n навмання взятих елементів. Тоді X набуває значень k=0,1,2,...,min(n,K) , а ймовірність їх появи визначається за гіпергеометричним законом
Нехай задано деяку множину однотипних елементів, число яких дорівнює N; з них K елементів мають, наприклад, ознаку А (колір, стандартність, наповнення), а решта N-K елементів — ознаку В. З цієї множини навмання беруть nелементів. Випадкова величина X – число елементів з ознакою А, що трапляється серед n навмання взятих елементів. Тоді X набуває значень k=0,1,2,...,min(n,K) , а ймовірність їх появи визначається за гіпергеометричним законом
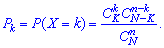
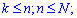
У табличній формі запису цей закон розподілу має вигляд
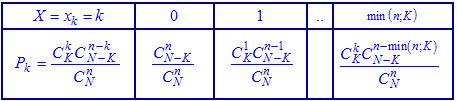 Нагадаємо, що сполучення знаходять за формулою
Нагадаємо, що сполучення знаходять за формулою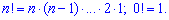
При n=k і k=0 сполучення рівне одиниці.
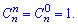 Умова нормування для гіпергеометричного розподілу має вигляд
Умова нормування для гіпергеометричного розподілу має вигляд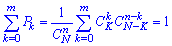 Залежно від умови задачі найменше значення може становити m = 0, 1, 2, 3, ..., m.
Залежно від умови задачі найменше значення може становити m = 0, 1, 2, 3, ..., m.
Числові характеристики цього закону обчислюються за наведеними нижче формулами:
1. Математичне сподівання
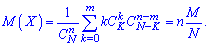
2. Дисперсія і середнє квадратичне відхилення
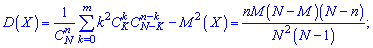
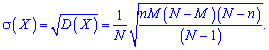
3. Формула для асиметрії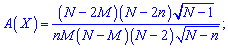 та ексцесу
та ексцесу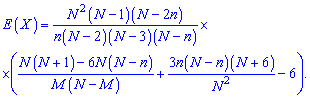 формули мають досить громіздкий вигляд, тому їх, як правило, обчислюють в екселі, чи математичних програмах (Maple, MathCad, Mathematica).
формули мають досить громіздкий вигляд, тому їх, як правило, обчислюють в екселі, чи математичних програмах (Maple, MathCad, Mathematica).
Розглянемо декілька прикладів на застосування наведених вище формул.
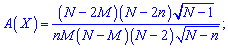 та ексцесу
та ексцесу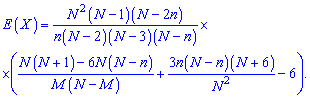 формули мають досить громіздкий вигляд, тому їх, як правило, обчислюють в екселі, чи математичних програмах (Maple, MathCad, Mathematica).
формули мають досить громіздкий вигляд, тому їх, як правило, обчислюють в екселі, чи математичних програмах (Maple, MathCad, Mathematica).Розглянемо декілька прикладів на застосування наведених вище формул.
Приклад 1. В ящику міститься 10 однотипних деталей, із них 7 стандартних, а решта є бракованими. Навмання із ящика беруть m деталей. Побудувати закони розподілу цілочислової випадкової величини Х — появу числа стандартних деталей серед m навмання взятих і обчислити математичне сподівання М(Х), дисперсію D (X), та середнє математичне відхилення S(Х), якщо:
I. m = 3;
II) m = 4;
III) m = 5;
IV) m = 7.
I. m = 3;
II) m = 4;
III) m = 5;
IV) m = 7.
Розв'язання. Використовуючи наведені вгорі формули побудуємо гіпергеометричні закони розподілу:
I. Маємо наступні початкові умови для випадку вибору трьох деталей
n = 3; N=10; K= 7; N-K= 3; k = 0, 1, 2, 3.
У табличній формі гіпергеометричний закон для цих даних має вигляд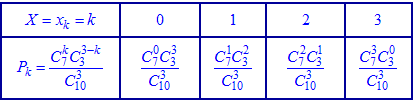 або після обчислення сполучень
або після обчислення сполучень
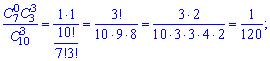
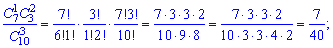
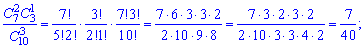
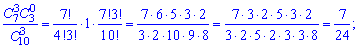
у вигляді таблиці ймовірностей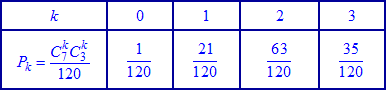 Умова нормування
Умова нормування
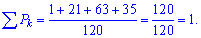
виконується, отже все вірно пораховано. Не лінуйтеся первіряти її, вона саме швидше вкаже Вам на присутність помилки при неправильній правій частині. Обчислюємо числові характеристики:
математичне сподівання
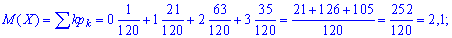
Дисперсію
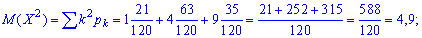
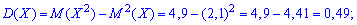
Середнє квадратичне відхилення
I. Маємо наступні початкові умови для випадку вибору трьох деталей
n = 3; N=10; K= 7; N-K= 3; k = 0, 1, 2, 3.
У табличній формі гіпергеометричний закон для цих даних має вигляд
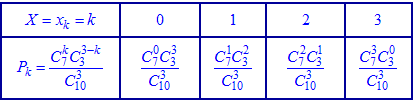 або після обчислення сполучень
або після обчислення сполучень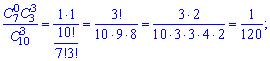
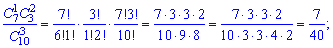
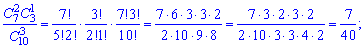
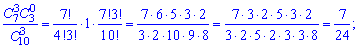
у вигляді таблиці ймовірностей
 Умова нормування
Умова нормування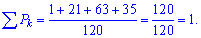
виконується, отже все вірно пораховано. Не лінуйтеся первіряти її, вона саме швидше вкаже Вам на присутність помилки при неправильній правій частині. Обчислюємо числові характеристики:
математичне сподівання
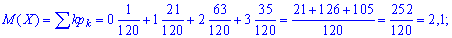
Дисперсію
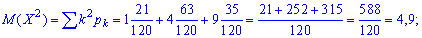
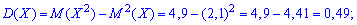
Середнє квадратичне відхилення
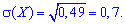
ІІ. Вибирають чотири деталі
n=4; K=7; N-K=3; k=1, 2, 3, 4.
У табличній формі закон розподілу запишеться формулами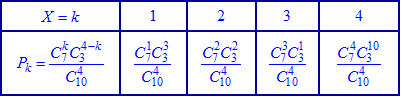 або після обчислень у вигляді таблиці
або після обчислень у вигляді таблиці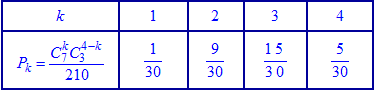 Перевіряємо умову нормування для знайдених значень.
Перевіряємо умову нормування для знайдених значень.
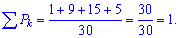
Вона виконується, отже можемо обчислювати числові характеристики за наведеними вище формулами:
математичне сподівання прийме значення
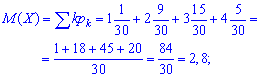
дисперсію і середнє квадратичне відхилення визначаємо за схемою попередньої задачі
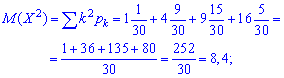
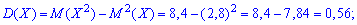
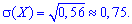
n=4; K=7; N-K=3; k=1, 2, 3, 4.
У табличній формі закон розподілу запишеться формулами
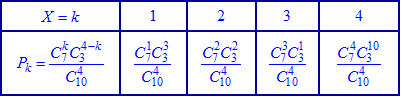 або після обчислень у вигляді таблиці
або після обчислень у вигляді таблиці Перевіряємо умову нормування для знайдених значень.
Перевіряємо умову нормування для знайдених значень.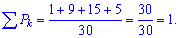
Вона виконується, отже можемо обчислювати числові характеристики за наведеними вище формулами:
математичне сподівання прийме значення
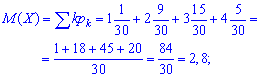
дисперсію і середнє квадратичне відхилення визначаємо за схемою попередньої задачі
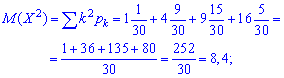
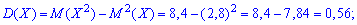
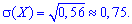
ІІІ. Вибирають п'ять деталей
т=5; K=7; N-K=3; k=2, 3, 4, 5.
У табличній формі закон подається так:
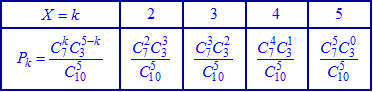 або після обчислень у вигляді таблиці значень
або після обчислень у вигляді таблиці значень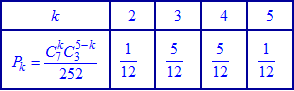 Умова нормування
Умова нормування
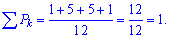
виконується. Обчислюємо математичне сподівання
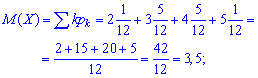
Складову дисперсії
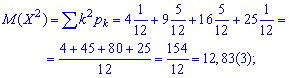
та саму дисперсію
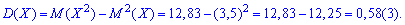 .
.
середнє квадратичне відхилення за відомою дисперсією
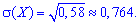
т=5; K=7; N-K=3; k=2, 3, 4, 5.
У табличній формі закон подається так:
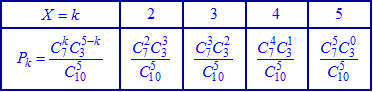 або після обчислень у вигляді таблиці значень
або після обчислень у вигляді таблиці значень Умова нормування
Умова нормування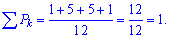
виконується. Обчислюємо математичне сподівання
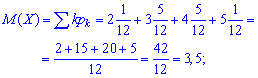
Складову дисперсії
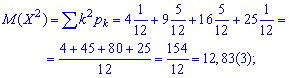
та саму дисперсію
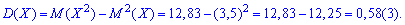 .
.середнє квадратичне відхилення за відомою дисперсією
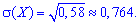
IV.) Вибирають сім деталей
т=7; K=7; N-K=3; k=4, 5, 6, 7.
т=7; K=7; N-K=3; k=4, 5, 6, 7.
У табличній формі даний розподіл приймає значення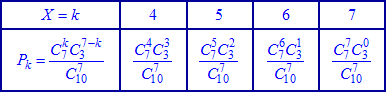 або після обчислень
або після обчислень
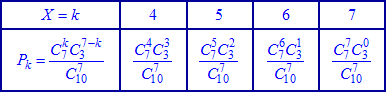 або після обчислень
або після обчислень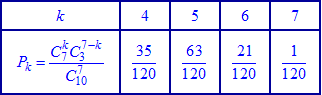
Умова нормування
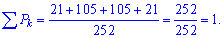
виконується.
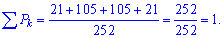
виконується.
Числові характеристики визначаємо на основі формул:
математичне сподівання
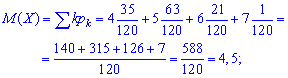
математичне сподівання квадрату величини
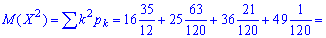
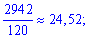
дисперсію
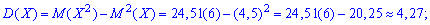
середнє квадратичне відхилення
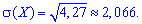
математичне сподівання
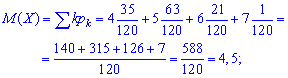
математичне сподівання квадрату величини
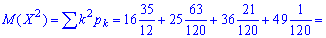
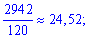
дисперсію
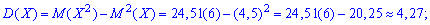
середнє квадратичне відхилення
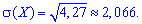
На цьому розв'язування задачі завершено. Будьте уважними при розв'язуванні прикладів на гіпергеометричний розподіл, оскільки досить часто потрібно знаходити сполучення 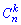 і при спрощенні факторіалів можна допустити помилку.
і при спрощенні факторіалів можна допустити помилку.
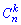 і при спрощенні факторіалів можна допустити помилку.
і при спрощенні факторіалів можна допустити помилку.
Немає коментарів:
Дописати коментар