Диференціювання. Правила та формули Нижче наведена таблиця містить основні формули диференціювання. З їх допомогою можна знайти більшість похідних і таблицю потрібно, якщо не знати на зубок, то хоча б мати під рукою для використання при вивченні диференціювання (знаходженні похідних). Запишемо правила знаходження похідних 1)  2)  3)  4)  5)  6) 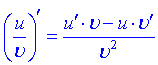 Тут С – стала величина (константа),  – функції від аргументу x, що мають похідні. 7) Якщо маємо– складену функція, тобто y=f(u), а u вссвою чергу фунція від аргументу, та існують окремо  похідні обидвох функцій  і , то існує похідна від y по x, причому Використовуючи це, таблицю формул похідних запишемо так 8) 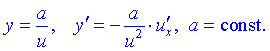 9)  10) 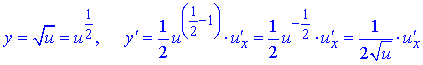 11)  12)  13) 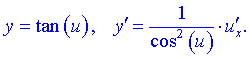 14) 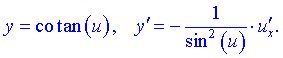 15) 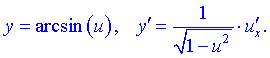 16) 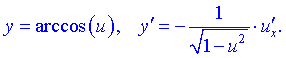 17) 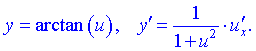 18) 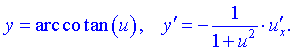 19)  20)  21) 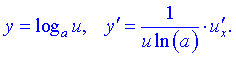 22) 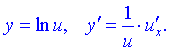 23)  В наступних статтях будуть наведені приклади диференціювання, враховуючи наведену таблицю. Якщо наведених формул похідних Вам мало, то можете знайти в інтернеті та завантажити довідник з "формулами диференціювання" та теоремами, які застосовують при знаходженні похідних

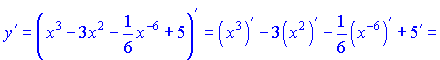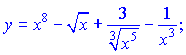
Знайти похідні за формулами диференціювання Для практичного ознайомлення з таблицею основних формул диференціювання розглянемо популярні варіанти завдань на похідні. Приклад 1. Обчислити похідні функцій 1)  Розв'язок. За формулами диференціювання (1), (3), (9) знаходимо похідну полінома Похідна від сталої рівна нулю. Це правило найлегше, тому запам'ятайте його в числі перших. 2)  Розв'язок. Вводимо дробові та від'ємні степені, та перетворюємо задану функцію до вигляду 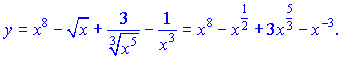Використовуючи формули (3), (4), (9), знаходимо похідні 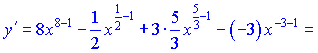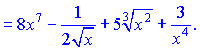Вкінці записуємо результат через корені. 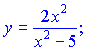3)  Розв'язок. 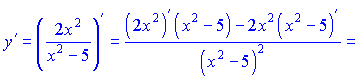Похідну дробової функції знаходимо за правилом похыдної частки 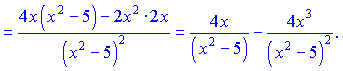Обчислення не складні - в результататі диференціювання отримаємо різницю простих дробів 1 та 2 типу. 4)  Розв'язок. 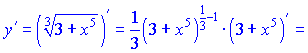Похідну кореневої залежності  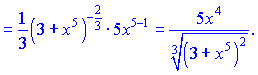шукаємо за правилом складної функції При роботі з дробовими показниками будьте уважні! 5)  Розв'язок. Похідну від добутку кореня на поліном знаходимо за правилом добутку функцій та формулою похідної від складної функції. 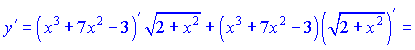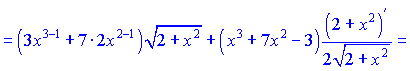В результаті отримаємо наступні перетворення 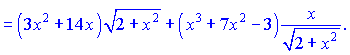Записів багатенько, проте на практиці буде не легше, тож вивчайте правили диференціювання. 6)  Розв'язок. За формулою похідної від складної функції отримаємо 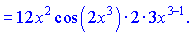Останній вираз можете спростити, підсумувавши показники змінної. 7) Розв'язок. Багато студентів, які ще добре не знають правил, спочатку підносять до квадрату вираз в дужках, а потім проводять диференціювання. Це неправильно, довго і важко. Скориставшись правилом диференціювання складної функції, отримаємо похідну від квадрату домножену на похідну кубічної функції Якщо Ви будете підносити до квадрату, а потім диференціювати то отримаєте многочлен, який ще треба буде зводити до компактного вигляду. Результат буде правильний, але навіщо йти складним шляхом, якщо за нас вже давно придумали правила диференціювання, які спрощують обчислення. Вивчайте їх та користуйтеся на практиці.

Метод логарифмічного диференціювання стає в нагоді при диференціюванні добутку кількох функцій або їх частки. Його зручно застосовувати при дифенеціюванні виразів, що містять корені із дробів (функцій), а також коли показник функції також являє собою складену функцію y=f(x)g(x) В таких випадках доцільно обидві частини виразу спочатку прологарифмувати за експонентою (e), а потім приступити до диференціювання. Цей спосіб одержав назву логарифмічного диференціювання. Похідну від логарифма функції називають логарифмічною похідною. Суть методу за допомогою формул можна описати наступним чином: маємо складну функцію вигляду y=t(x); до обох сторін застосовуємо логарифмування ln(y)=ln(t(x)) і знаходимо похідні правої і лівої частини рівності у вигляді формул 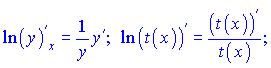Прирівнюємо похідні і виражаємо y' 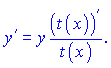В цьому вся суть методу, далі все залежить від функції t(x). Якщо t(x) задана добутком функцій то за властивостями логарифма при диференціюванні отримаємо суму логарифмів Якщо маємо дробову функцію 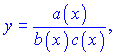то, застосовуючи логарифмування, отримаємо різницю логарифмів 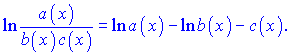Якщо маємо складену показникову функцію (функція в степені іншої) то за властивостями логарифма отримаємо залежність У випадку коренів (g(x)=С=1/2; 1/3, ...) диференціювання значно спрощується і отриамємо добуток показника на огарифм Подальше обчислення похідних залежить від складності самих функцій. Розглянемо конкретні завдання, щоб даний матеріал став для Вас більш зрозумілішим і наочнішим. Приклад 1. Використовуючи логарифмування знайти похідну  (Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" ) 1) (5.2.178) у = х 5x Розв'язок. Приклади вибрано складні для того, щоб розкрити всю силу методу логарифмічного диференціювання та розглянути поширені для студентсьої практики приклади. Проведемо логарифмування лівої і правої частин Далі знайдемо похідну добутку функцій Похідна лівої частини показана при викладі теоретичного матеріалу. Записуємо результати обчислень 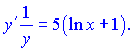Далі переносимо функцію y із знаменника в праву частину та не забуваємо замінити її значення на вихідне Незважаючи на складний вигляд даний приклад розв'язано. 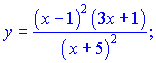2) (5.2.191) Розв'язок.Знаходимо логарифм дробової функції 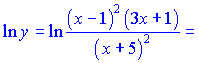Проводимо диференціювання обох частин залежності 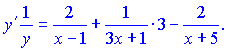Зведемо під спільний знаменник праву сторону. В результаті математичних операцій отримаємо 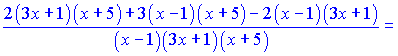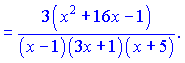Підставимо в вихідну формулу, перенісши функцію в праву частину 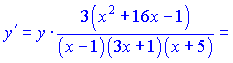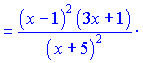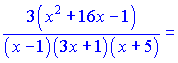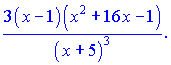В результаті ряду нескладних маніпуляцій отримали досить компактний кінцевий результат похідної. При обчисленні даного прикладу напряму подібний результат довелося б шукати дуже довго. 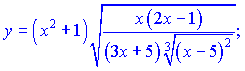3) (5.2.195) Розв'язок.Незважаючи на складний вигляд, дану функцію на основі властивостей поазників можна переписати у вигляді 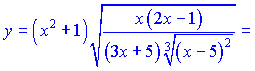Застосуємо логарифмування Похідна від правої частини рівна 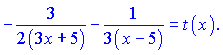Тут для спрощення подальших викладок позначии резуьтат диференціювання через t(x). Враховуючи похідну від ln(y), остаточно отримаємо 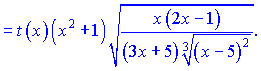Можна залишати в такому вигляді, оскільки суть даного уроку навчитися застосовувати метод логарифмічного диференціювання. Проте, якщо Ви захочете для спрощення звести все до спільного знаменника, то отримаєте таку відповідь 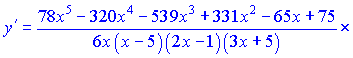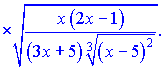Повірте - це займе у Вас чимало часу 4) (5.2.199) Розв'язок.Проводимо логарифмування функції Далі за наведеною схемою знаходимо диференціюємо праву частину залежності 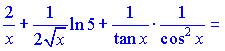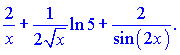Підставивши в формулу для похідної від логарифма, отримаємо 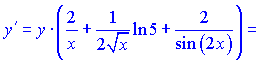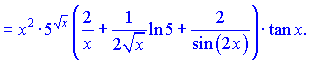На цьому розв'язування прикладу завершено. Практикуйте з подібними завданнями і через певний час у Вас не буде жодних труднощів із знаходженням похідної через огарифмування функції. Знаходження похідних від неявно заданих функцій Часто на практиці зустрічаються функції, в яких незалежна змінна x і функція y зв'язані між собою формулою f(x,y)=0 з якої не можна відокремити саму функцію. В цьому випадку функція y(x) називається неявною функцією від аргумента x. Однак саму похідну від функції по змінній x можна обчислити. Для цього диференціюють функцію f(x,y) по x, при цьому враховують, що сама функція залежна від змінної y=y(x). З одержаного рівняння згруповують доданки, що містяться при похідній y' і виражають її. Як це виглядає на пракиці проілюстровано на прикладах із Дубовика В.П., Юрика І.І. "Вища математика. Збірник задач". Приклад 1. Знайти похідні неявно від заданих функцій y(x) . 1) (5.219) 3 x +3 y = 3 x-y Розв'язок:Продиференціюємо праву і ліву частини Отриманий вираз поділимо на спільний множник ln(3) та згрупуємо доданки, що містять похідну y'(x) і перенесемо їх в одну сторону за знак рівності. В результаті отримаємо Поділивши на множник при похідній y'(x) отримаємо її значення 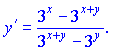Для спрощення винесемо із чисельника та знаменника спільні множники 3x та 3y відповідно. В результаті отримаємо: 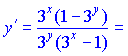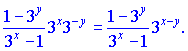Як бачите, нічого складного ми не робили, проте швидко відшукали похідну неявно заданої функції. Розглянемо наступне завдання. 2) (5.223) Розв'язок:Проведемо диференціювання виразу. Перший доданок дасть 2, похідну від арккосинуса знаходимо за правилом складеної фунції 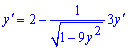Виділяємо доданки, що містять похідну y'(x) 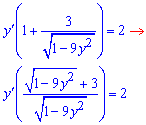Поділимо на множник при похідній та відшукаємо її значення 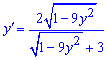Завдання повністю розв'язане. 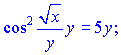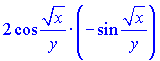3) (5.227) Розв'язок:Обчислимо похідну правої і лівої частини, від косинуса знаходимо, як від складеної функції 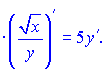Похідну від частки функцій рівна 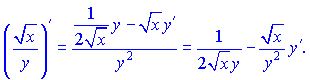Перших два множники рівні синусу подвійного кута. Тому похідні можемо згрупувати у вигляді 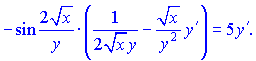Домножимо праву та ліву частини на множник 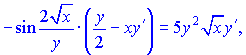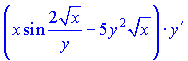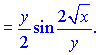, щоб позбутися знаменників та згрупуємо доданки при похідній y'(x) З останньої залежності знаходимо значення потрібної похідної 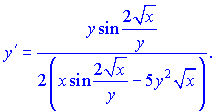В такого роду прикладах головне не помилитися при відшуканні похідних. Фугкції тут взято доволі складні, заодно вивчете інші правила диференціювання. 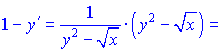4) (5.236) Розв'язок:Диференціюємо неявно задану функцію по змінній 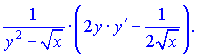Перегрупуємо доданки, що містять y' 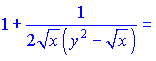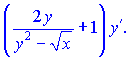Зводимо вирази до спільного знаменника 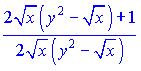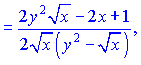та підставляємо їх на свої місця 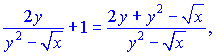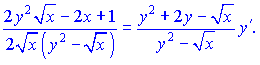Звідси виражаємо похідну функції 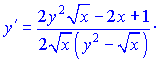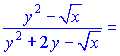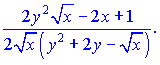На цьому завдання розв'язано. При обчисленні похідної неявно заданої функції типовими помилками на практиці є неправильне взяття похідної та плутанина зі знаками при групуванні подібних доданків. Будьте уважні в таких ситуаціях та не допускайте помилок. На скадних умовах Ви побачили як брати похідну від неявно заданої функцій, тому, якщо попрацюєте самостійно, то з даної теми отримаєте хороші результати на тастах, контрольних.

Знаходження похідних від неявно заданих функцій

Параметрично задана функція. Правила та приклади знаходження похідної

Часткові похідні першого та другого порядку

Знаходження похідних вищих порядків

Механічний зміст похідної. Розв'язування задач

Геометричний зміст похідної. Дотична та нормаль до кривої

Диференціал. Приклади наближених обчислень

Диференціал довжини дуги

Кривина плоскої кривої. Радіус кривини