Кривина плоскої кривої. Радіус кривини
Плоскою кривою називають лінію, всі точи якої лежать в одній площині. Кривина плоскої кривої визначає ступінь її відхилення від прямої і в декартовій системі координат y=f(x) визначається залежністю
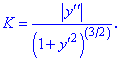
Кривина кривої визначається в кожній її точці. Якщо крива задана параметрично 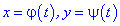 то кривина визначається залежністю
то кривина визначається залежністю
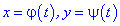 то кривина визначається залежністю
то кривина визначається залежністю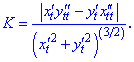
У полярних координатах кривина лінії 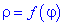 обчислюється за формулою
обчислюється за формулою
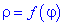 обчислюється за формулою
обчислюється за формулою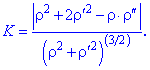
Радіусом кривини лінії є величина, обернена до кривини
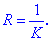
Радіус кривини рівний радіусу дотичного кола в заданій точці. Центр цього кола називається центром кривини, а його координати M(x0; y0) знаходять за формулами
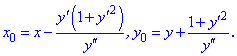
Коло, центр якого співпадає з центром кривини лінії в даній точці M(x0; y0) і з радіусом, що рівний радіусу кривини, називається колом кривини лінії в цій точці.
Еволюта лінії – це геометричне місце центрів її кривини.
Еволюта лінії – це геометричне місце центрів її кривини.
Розглянемо приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" для засвоєння матеріалу на практиці.
Приклад 1. Знайти кривини ліній.
(5.983)y=x4-8x3+20x-12 в точці (1;1).
Розв'язок. Знайдемо першу та другу похідну функції
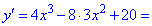
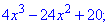
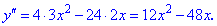
Обчислюємо значення похідних в заданій точці
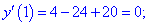
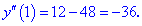
Результати підставляємо в формулу кривини кривої
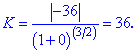
На цьому приклад розв'язано і як можна бачити обчислення не складні.
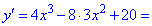
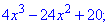
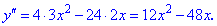
Обчислюємо значення похідних в заданій точці
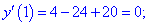
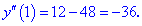
Результати підставляємо в формулу кривини кривої
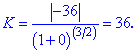
На цьому приклад розв'язано і як можна бачити обчислення не складні.
(5.986)y=ln(1+x2) у початку координат.
Розв'язок. Обчислюємо похідну логарифма
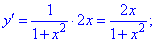
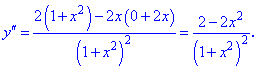
Знаходимо значення похідних в початку координат
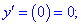
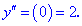
Знайдені величини підставляємо в рівняння кривини кривої
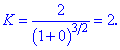
Кривина рівна 2.
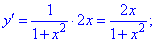
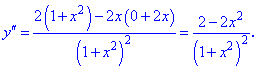
Знаходимо значення похідних в початку координат
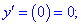
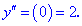
Знайдені величини підставляємо в рівняння кривини кривої
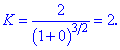
Кривина рівна 2.
(5.990) 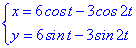 в точці t=Pi/3.
в точці t=Pi/3.
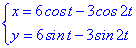 в точці t=Pi/3.
в точці t=Pi/3.
Розв'язок. Знаходимо похідні параметрично заданої функції
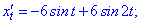
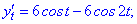
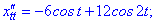
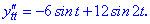
Знаходимо значення похідних в заданій точці
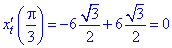
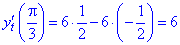
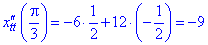
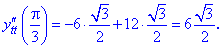
Отримані значення підставляємо в формулу
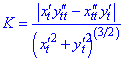
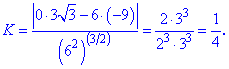
Кривина рівна 1/4.
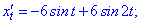
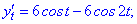
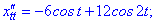
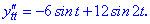
Знаходимо значення похідних в заданій точці
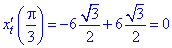
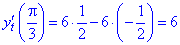
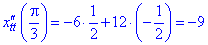
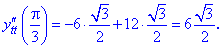
Отримані значення підставляємо в формулу
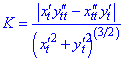
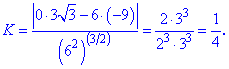
Кривина рівна 1/4.
(5.993) 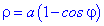 при
при 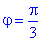 .
.
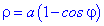 при
при 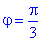 .
.
Розв'язок. Знаходимо першу та другу похідну функції, заданої в полярній системі координат
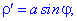
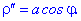
При заданому куті функція та похідні приймуть наступні значення:
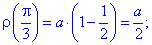
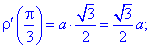
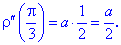
Кривину в полярній системі координат визначаємо за формулою
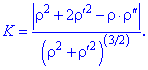
Знайдені значення функції та похідних підставляємо в співвідношення та обчислюємо
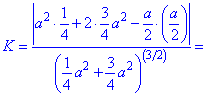
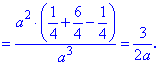
Практична сторона обчислення кривини плоскої кривої полягає у відшуканні значень першої та другої похідної в заданій точці. Якщо Вам без труднощів вдається диференціювати функції, то обчислювати кривину та радіус кривини Ви навчитеся без великих зусиль.
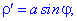
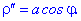
При заданому куті функція та похідні приймуть наступні значення:
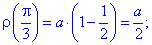
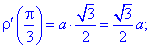
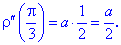
Кривину в полярній системі координат визначаємо за формулою
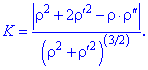
Знайдені значення функції та похідних підставляємо в співвідношення та обчислюємо
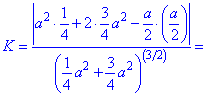
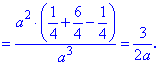
Практична сторона обчислення кривини плоскої кривої полягає у відшуканні значень першої та другої похідної в заданій точці. Якщо Вам без труднощів вдається диференціювати функції, то обчислювати кривину та радіус кривини Ви навчитеся без великих зусиль.
Немає коментарів:
Дописати коментар