Рівномірний закон розподілу. Приклади
Цілочислова випадкова величина Х має рівномірний закон розподілу, якщо ймовірності її можливих значень однакова від експерименту до експерименту і обчислюються формулою
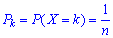 У табличній формі запису рівномірний закон розподілу має вигляд:
У табличній формі запису рівномірний закон розподілу має вигляд:
 Умова нормування для рівномірного закону розподілу має вигляд
Умова нормування для рівномірного закону розподілу має вигляд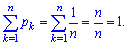 Імовірнісна твірна функція на основі першої формули приймає значення
Імовірнісна твірна функція на основі першої формули приймає значення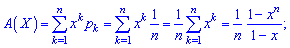
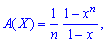 або
або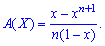 Числові характеристики рівномірного закону знаходимо на основі твірної функції
Числові характеристики рівномірного закону знаходимо на основі твірної функції
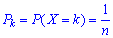 У табличній формі запису рівномірний закон розподілу має вигляд:
У табличній формі запису рівномірний закон розподілу має вигляд: Умова нормування для рівномірного закону розподілу має вигляд
Умова нормування для рівномірного закону розподілу має вигляд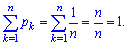 Імовірнісна твірна функція на основі першої формули приймає значення
Імовірнісна твірна функція на основі першої формули приймає значення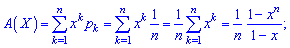
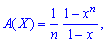 або
або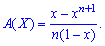 Числові характеристики рівномірного закону знаходимо на основі твірної функції
Числові характеристики рівномірного закону знаходимо на основі твірної функції
1. Математичне сподівання знаходимо за формулою
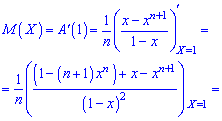
При х = 1 отримуємо невизначеність (0/0), яку розкриваємо за правилом Лопіталя
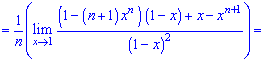
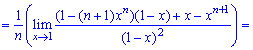
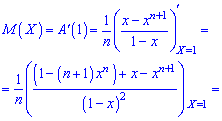
При х = 1 отримуємо невизначеність (0/0), яку розкриваємо за правилом Лопіталя
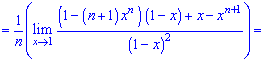
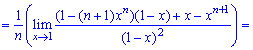
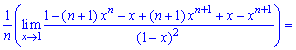
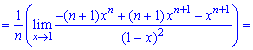
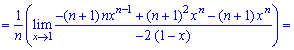
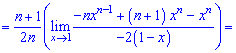
При х = 1 знову маємо невизначеність виду (0/0), яку також розкриваємо за правилом Лопіталя
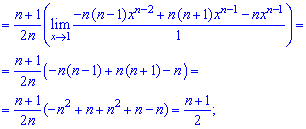
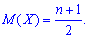 Обчислення зайняли багата часу, однак формула для математичного сподівання вийшла досить легкою.
Обчислення зайняли багата часу, однак формула для математичного сподівання вийшла досить легкою.
2. Виконавши подібні, але більш громіздкі перетворення, дисперсію і середнє математичне відхилення знаходимо за готовими формулами
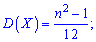
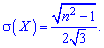
3. Для рівномірного розподілу ймовірностей асиметрія і ексцес рівні нулю
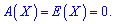
Є й інше означення, згідно з яким функція має рівномірний розподіл, якщо на деякому інтервалі щільність імовірностей приймає постійне значення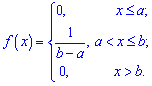 Функція розподілу ймовірностей для рівномірного закону визначається інтегруванням
Функція розподілу ймовірностей для рівномірного закону визначається інтегруванням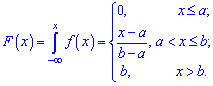 Математичне сподівання в таких випадках визначають залежністю
Математичне сподівання в таких випадках визначають залежністю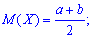 дисперсію за формулою
дисперсію за формулою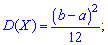 і середнє квадратичне відхилення через корінь
і середнє квадратичне відхилення через корінь Ймовірність влучання випадкової величини Х в деякий інтервал
Ймовірність влучання випадкової величини Х в деякий інтервал 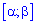 , який міститься всередині інтервалу
, який міститься всередині інтервалу 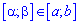 визначається за формулою
визначається за формулою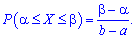 Наведені формули часто є більш застосовуваними на практиці ніж ті, що були дані вище.
Наведені формули часто є більш застосовуваними на практиці ніж ті, що були дані вище.
Розглянемо приклади відшукання числових характеристик.
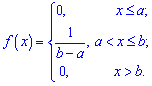 Функція розподілу ймовірностей для рівномірного закону визначається інтегруванням
Функція розподілу ймовірностей для рівномірного закону визначається інтегруванням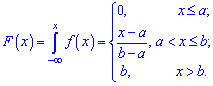 Математичне сподівання в таких випадках визначають залежністю
Математичне сподівання в таких випадках визначають залежністю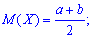 дисперсію за формулою
дисперсію за формулою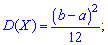 і середнє квадратичне відхилення через корінь
і середнє квадратичне відхилення через корінь Ймовірність влучання випадкової величини Х в деякий інтервал
Ймовірність влучання випадкової величини Х в деякий інтервал 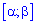 , який міститься всередині інтервалу
, який міститься всередині інтервалу 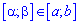 визначається за формулою
визначається за формулою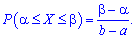 Наведені формули часто є більш застосовуваними на практиці ніж ті, що були дані вище.
Наведені формули часто є більш застосовуваними на практиці ніж ті, що були дані вище.Розглянемо приклади відшукання числових характеристик.
Приклад 1. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення М (Х), D (X), S (Х), якщо цілочислова випадкова величина Х має рівномірний закон розподілу і можливі значення її значення лежать в діапазоні 1..50:
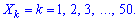 .
.
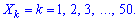 .
.
Розв'язання. За умовою задачі маємо такі дані n = 50, p = 1/50=0,02.
Згідно формул обчислюємо математичне сподівання
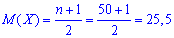
дисперсія
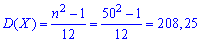
середнє квадратичне відхилення
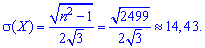
Згідно формул обчислюємо математичне сподівання
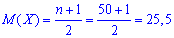
дисперсія
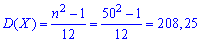
середнє квадратичне відхилення
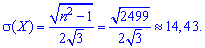
Приклад 2. Поїзда в метро прибувають на станцію кожні 10 хвилин. Визначити ймовірність того, що час очікування поїзда не буде більшим за 4 хвилини.
Розв'язання. За умовою задачі маємо два інтервали
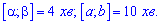
Згідно формули, шукана ймовірність рівна частці цих величин
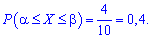
Задачі на відшукання інтервалу попадання випадкової величини, що розподілена за рівнимірним законом розв'язуйте за такою ж схемою. Вона проста і не вимагає складних обчислень.
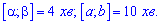
Згідно формули, шукана ймовірність рівна частці цих величин
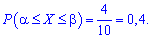
Задачі на відшукання інтервалу попадання випадкової величини, що розподілена за рівнимірним законом розв'язуйте за такою ж схемою. Вона проста і не вимагає складних обчислень.
Немає коментарів:
Дописати коментар