Криволінійний інтеграл ІІ роду. Робота силового поля
Задачі на знаходження роботи силового поля з переміщення матеріальної точки вирішуюють застосуванням криволінійного інтегралу ІІ роду. Щоб не повторювати в кожній новій статті на криволінійні інтеграли ті ж формули зразу переходимо до аналізу готових прикладів.
Обчислення роботи силового поля за допомогою криволінійного інтегралу ІІ роду
ЗАВДАННЯ 3.5 Обчислити роботу силового поля 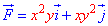 з переміщення матеріальної точки вздовж лінії L: x2+y2=4 від точки A(2;0) до точки B(0;2).
з переміщення матеріальної точки вздовж лінії L: x2+y2=4 від точки A(2;0) до точки B(0;2).
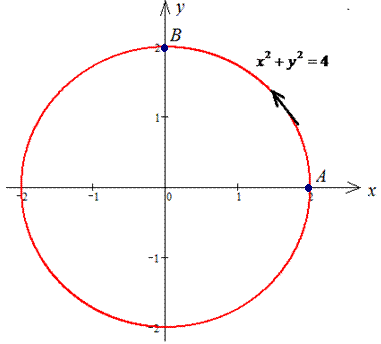
Розв'язання: Побудуємо в декартових координатах траєкторію матеріальної точки вздовж кола L: x2+y2=4.
Рівняння верхньої частини півкола та її похідної рівні
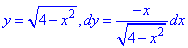
Відповідно до точок A(2;0), B(0;2) межі інтегрування змінюються від 2 до 0. Не дивуйтеся, що не в зворотньому порядку. Їх завжди потрібно виписувати в порядку обходу контуру від точки A до B.
Робота силового поля F з переміщенн матеріальної точки вздовж лінії L обчислюється за допомогою криволінійного інтеграла ІІ роду:
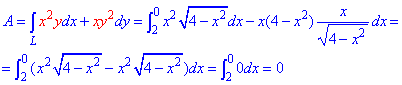
Уважно перегляньте рівняння силового поля та підінтегральну функцію і Вам стане зрозуміло, що і звідки береться. Як обчислити криволінійний інтеграл детально розписано в попередніх статтях (заміняємо y,dy на ф-ї від "х"під інтегралом).
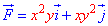 з переміщення матеріальної точки вздовж лінії L: x2+y2=4 від точки A(2;0) до точки B(0;2).
з переміщення матеріальної точки вздовж лінії L: x2+y2=4 від точки A(2;0) до точки B(0;2).Розв'язання: Побудуємо в декартових координатах траєкторію матеріальної точки вздовж кола L: x2+y2=4.

Рівняння верхньої частини півкола та її похідної рівні
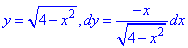
Відповідно до точок A(2;0), B(0;2) межі інтегрування змінюються від 2 до 0. Не дивуйтеся, що не в зворотньому порядку. Їх завжди потрібно виписувати в порядку обходу контуру від точки A до B.
Робота силового поля F з переміщенн матеріальної точки вздовж лінії L обчислюється за допомогою криволінійного інтеграла ІІ роду:
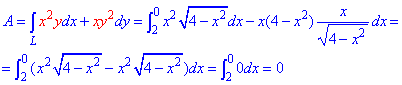
Уважно перегляньте рівняння силового поля та підінтегральну функцію і Вам стане зрозуміло, що і звідки береться. Як обчислити криволінійний інтеграл детально розписано в попередніх статтях (заміняємо y,dy на ф-ї від "х"під інтегралом).
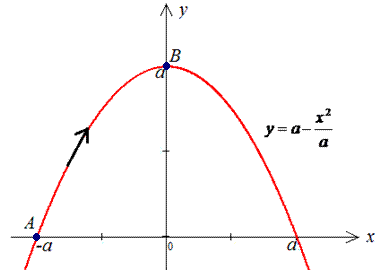
ЗАВДАННЯ 3.10 Обчислити роботу силового поля 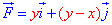 по переміщенню матеріальної точки вздовж лінії L: y=a-x2/a від точки A(-a;0) до точки B(0;a).
по переміщенню матеріальної точки вздовж лінії L: y=a-x2/a від точки A(-a;0) до точки B(0;a).
Розв'язання: Маємо y=a-x2/a - рівняння параболи, знаходимо диференціал dy=-2x/a*dx і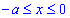 .
.
Обчислюємо роботу силового поля F, потрачену на переміщенню матеріальної точки вздовж лінії L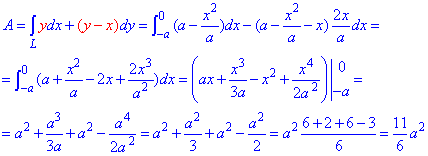
Криволінійний інтеграл ІІ роду знаходимо за першою формулою інтегрування.
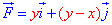 по переміщенню матеріальної точки вздовж лінії L: y=a-x2/a від точки A(-a;0) до точки B(0;a).
по переміщенню матеріальної точки вздовж лінії L: y=a-x2/a від точки A(-a;0) до точки B(0;a).Розв'язання: Маємо y=a-x2/a - рівняння параболи, знаходимо диференціал dy=-2x/a*dx і
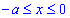 .
.
Обчислюємо роботу силового поля F, потрачену на переміщенню матеріальної точки вздовж лінії L
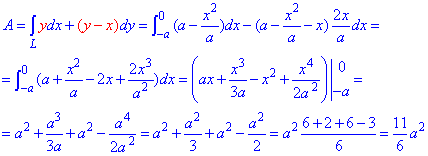
Криволінійний інтеграл ІІ роду знаходимо за першою формулою інтегрування.
ЗАВДАННЯ 3.12 Обчислити роботу силового поля 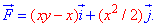 по переміщенню матеріальної точки вздовж лінії L:
по переміщенню матеріальної точки вздовж лінії L: 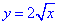 від точки A(0;0) до точки B(1;2). .
від точки A(0;0) до точки B(1;2). .
Розв'язання: Будуємо траєкторію матеріальної точки вздовж кореневої лінії L: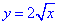 .
.
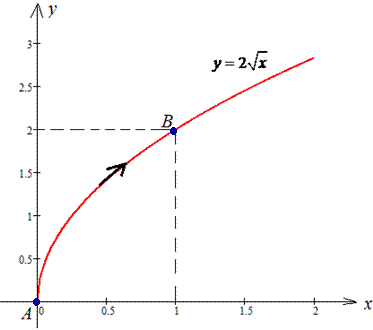
Записуємо похідну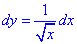 та проміжок інтегрування [0;1].
та проміжок інтегрування [0;1].
За допомогою криволінійного інтегралу ІІ роду знаходимо роботe A силового поля F :
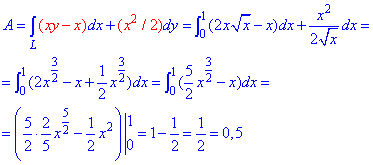
Перед інтегруванням перетворюємо корені до показникової форми запису, а далі обчислюємо за табличними формулами.
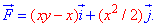 по переміщенню матеріальної точки вздовж лінії L:
по переміщенню матеріальної точки вздовж лінії L: 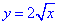 від точки A(0;0) до точки B(1;2). .
від точки A(0;0) до точки B(1;2). .Розв'язання: Будуємо траєкторію матеріальної точки вздовж кореневої лінії L:
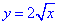 .
.
Записуємо похідну
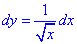 та проміжок інтегрування [0;1].
та проміжок інтегрування [0;1].За допомогою криволінійного інтегралу ІІ роду знаходимо роботe A силового поля F :
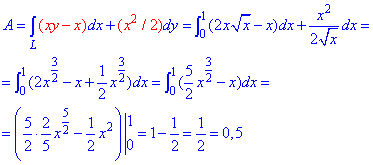
Перед інтегруванням перетворюємо корені до показникової форми запису, а далі обчислюємо за табличними формулами.
ЗАВДАННЯ 3.14 Обчислити роботу силового поля 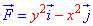 по переміщенню матеріальної точки вздовж лінії L: x2+y2=9.
по переміщенню матеріальної точки вздовж лінії L: x2+y2=9.
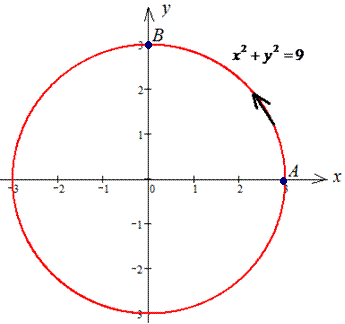
Розв'язання: Наведемо траєкторію руху матеріальної точки по колу L: x2+y2=9.
Верхня вітка обмежена функцією
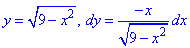
Аргумент змінюється від 3 до 0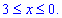
Робота А силового поля F з переміщенню матеріальної точки вздовж лінії L обчислюється за допомогою криволінійного інтеграла ІІ роду: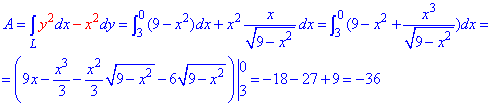
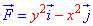 по переміщенню матеріальної точки вздовж лінії L: x2+y2=9.
по переміщенню матеріальної точки вздовж лінії L: x2+y2=9.Розв'язання: Наведемо траєкторію руху матеріальної точки по колу L: x2+y2=9.

Верхня вітка обмежена функцією
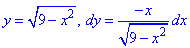
Аргумент змінюється від 3 до 0
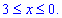
Робота А силового поля F з переміщенню матеріальної точки вздовж лінії L обчислюється за допомогою криволінійного інтеграла ІІ роду:
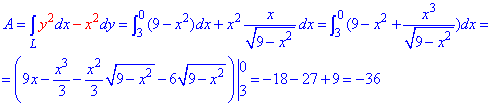
Інтегрування саме по собі не важке, головне правильно знайти диференціал функції та не помилитися з межами інтегрування.
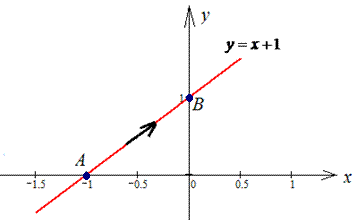
ЗАВДАННЯ 3.19 Обчислити роботу силового поля 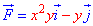 з переміщення матеріальної точки вздовж лінії L: пряма від точки A(-1;0) до точки B(0;1).
з переміщення матеріальної точки вздовж лінії L: пряма від точки A(-1;0) до точки B(0;1).
Розв'язання: Запишемо рівняння прямої, що проходить через дві точки A(-1;0) і B(0;1):
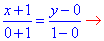
звідси y=x+1.
Таким чином, маємо диференціал дуги dy=dx, та інтервал [-1;0].
Графік прямої наведено на рисунку
Визначаємо роботу силового поля F з переміщення матеріальної точки вздовж лінії L: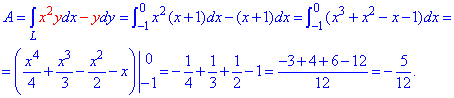
Криволінійний інтеграл 2 порядку легко зводимо до визначеного та знаходимо результуюче значення роботи.
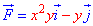 з переміщення матеріальної точки вздовж лінії L: пряма від точки A(-1;0) до точки B(0;1).
з переміщення матеріальної точки вздовж лінії L: пряма від точки A(-1;0) до точки B(0;1).Розв'язання: Запишемо рівняння прямої, що проходить через дві точки A(-1;0) і B(0;1):
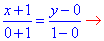
звідси y=x+1.
Таким чином, маємо диференціал дуги dy=dx, та інтервал [-1;0].
Графік прямої наведено на рисунку

Визначаємо роботу силового поля F з переміщення матеріальної точки вздовж лінії L:
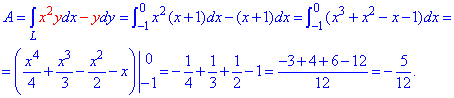
Криволінійний інтеграл 2 порядку легко зводимо до визначеного та знаходимо результуюче значення роботи.
ЗАВДАННЯ 3.20 Обчислити роботу силового поля 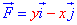 по переміщенню матеріальної точки вздовж лінії L: x2+y2=1 від точки A(1;0) до точки B(-1;0).
по переміщенню матеріальної точки вздовж лінії L: x2+y2=1 від точки A(1;0) до точки B(-1;0).
Розв'язання: Побудуємо траєкторію матеріальної точки проти руху годинникової стрілки за колом L: x2+y2=9.
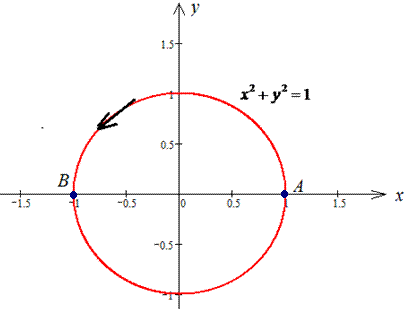
Верхня його дуга описується кореневою залежністю
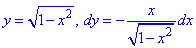
Аргумент при цьому змінюється від 1 до -1.
Робота силового поля витрачена на переміщенню матеріальної точки вздовж дуги кола рівна інтегралу: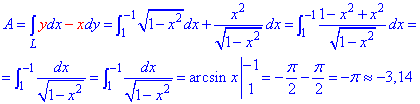
Під час інтегрування отримаємо арксинус, який на границях дає число Pi/2.
Ще один розділ де можна застосувати криволінійний інтеграл ІІ роду від тепер доступний та відомий Вам.
Будьте уважні в обчисленнях і успішного Вам навчання!
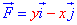 по переміщенню матеріальної точки вздовж лінії L: x2+y2=1 від точки A(1;0) до точки B(-1;0).
по переміщенню матеріальної точки вздовж лінії L: x2+y2=1 від точки A(1;0) до точки B(-1;0).Розв'язання: Побудуємо траєкторію матеріальної точки проти руху годинникової стрілки за колом L: x2+y2=9.

Верхня його дуга описується кореневою залежністю
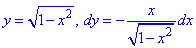
Аргумент при цьому змінюється від 1 до -1.
Робота силового поля витрачена на переміщенню матеріальної точки вздовж дуги кола рівна інтегралу:
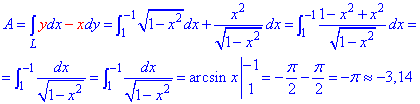
Під час інтегрування отримаємо арксинус, який на границях дає число Pi/2.
Ще один розділ де можна застосувати криволінійний інтеграл ІІ роду від тепер доступний та відомий Вам.
Будьте уважні в обчисленнях і успішного Вам навчання!
Немає коментарів:
Дописати коментар