Диференціал довжини дуги
Диференціал дуги плоскої кривої характеризує приріст її довжини за короткий проміжок зміни і в декартовій системі координат визначається залежністю
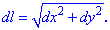
Якщо крива задана у вигляді функціональної залежності y=f(x) то диференціал дуги визначаємо за формулою
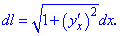
При параметричному задані функції отримаємо наступні залежності
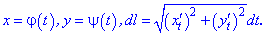
Якщо лінія задана в полярній системі координат, то диференціал дуги обчислюємо за формулою
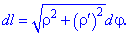
З формул бачимо, що при обчисленнях потрібно знаходити похідні першого порядку.
Розглянемо приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Знайти диференціал дуги ліній:
(5.966) 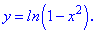
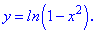
Розв'язок. Знаходимо диференціал довжини дуги за формулою
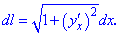
Для цього обчислюємо похідну функції
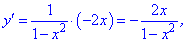
та підставляємо знайдене значення у формулу
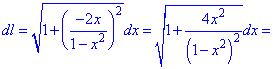
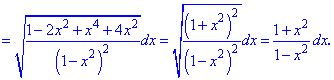
Ось така вийде залежність довжини дуги від змінної.
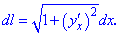
Для цього обчислюємо похідну функції
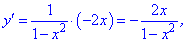
та підставляємо знайдене значення у формулу
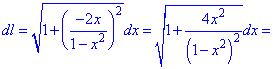
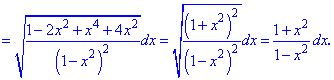
Ось така вийде залежність довжини дуги від змінної.
(5.972) 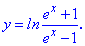
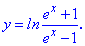
Розв'язок. Проводимо диференціювання логарифма, як складеної функції. Тут ще маємо і дробову функцію і експоненту, так що слідкуйте за обчисленнями
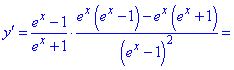
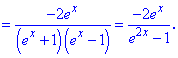
Знайдену похідну підставляємо в формулу для обчислення диференціалу дуги
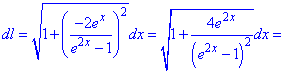
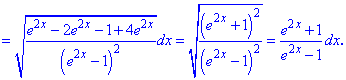
Після групування та зведення до повних квадратів корені скоротяться.
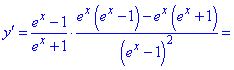
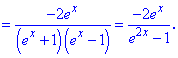
Знайдену похідну підставляємо в формулу для обчислення диференціалу дуги
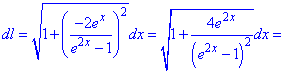
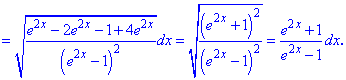
Після групування та зведення до повних квадратів корені скоротяться.
(5.973) 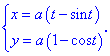
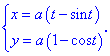
Розв'язок. Маємо параметрично задану функцію, для знаходження її диференціалу дуги обчислюємо похідні від аргументу x та змінної y за параметром t
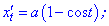
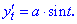
Отримані значення підставляємо в формулу диференціалу дуги
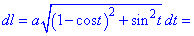
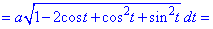
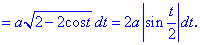
Скориставшись формулою дя косинусів, записали залежність в компактному вигляді.
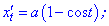
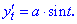
Отримані значення підставляємо в формулу диференціалу дуги
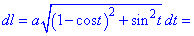
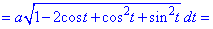
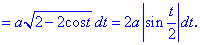
Скориставшись формулою дя косинусів, записали залежність в компактному вигляді.
(5.974) 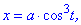
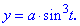
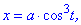
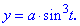
Розв'язок. Астроїда задана параметричним рівнянням. Знаходимо похідні
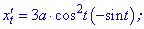
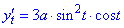
Обчислюємо диференціал дуги, попередньо винісши за знак кореня спільні множники
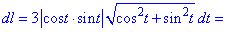
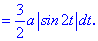
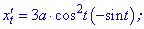
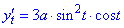
Обчислюємо диференціал дуги, попередньо винісши за знак кореня спільні множники
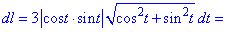
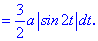
(5.975) 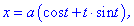
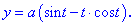
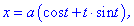
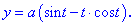
Розв'язок. Обчислюємо похідні параметрично заданої функції
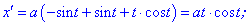
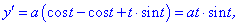
та підставляємо у формулу для визначення диференціалу довжини дуги
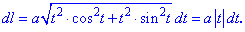
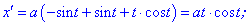
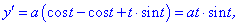
та підставляємо у формулу для визначення диференціалу довжини дуги
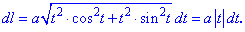
(5.979) 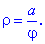
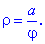
Розв'язок. Дана функція задана в полярній системі координат, тому її диференціал дуги визначаємо за останньою з наедених вгорі формул
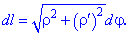
Знаходимо похідну по радіусу
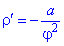
та підставляємо в корінь квадратний
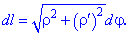
Знаходимо похідну по радіусу
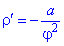
та підставляємо в корінь квадратний
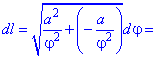
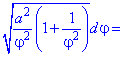
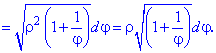
Після спрощень отримаємо диференціал довжини дуги.
(5.980) 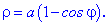 (кардіоїда)
(кардіоїда)
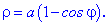 (кардіоїда)
(кардіоїда)
Розв'язок. Обчислюємо похідну функції в полярних координатах
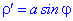
та знаходимо приріст довжини дуги від кута
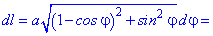
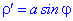
та знаходимо приріст довжини дуги від кута
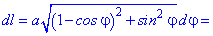
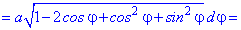
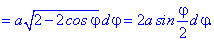
Розв'язані приклади знаходження диференціалу довжини дуги ривих, які задані в декартовій та полярній системах координат, а також параметрично показали, що основним в обчисленні є вміння диференціювати функції. Все решта зводиться до спрощень та відшукання коренів. Користуйтеся формулами для обчислення диференціалу довжини дуги, вивчайте формули похідних, правила диференціювання і розв'язування подібних прикладів не будеважким для Вас.
Немає коментарів:
Дописати коментар