Знаходження тригонометричних інтегралів вигляду sin(kx)cos(lx), cos(kx)cos(lx), sin(kx)sin(lx)
Інтеграли від тригонометричних функцій вигляду sin(kx)*cos(lx), cos(kx)*cos(lx), sin(kx)*sin(lx)
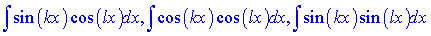
де k не рівне l дійсні числа, зводяться до табличних інтегралів за допомогою тригонометричних формул
І.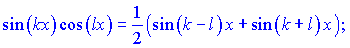
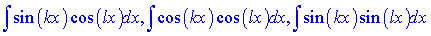
де k не рівне l дійсні числа, зводяться до табличних інтегралів за допомогою тригонометричних формул
І.
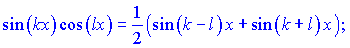
ІІ.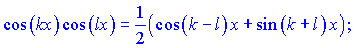
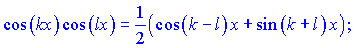
ІІІ. 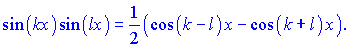
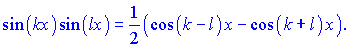
Розв'яжемо приклади, щоб показати кожне з правил на практиці.
Приклад 1. Обчислити інтеграли
а) 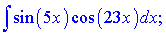
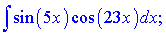
Розв'язок: Підінтегральну функцію за І правилом запишемо у вигляді
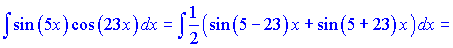
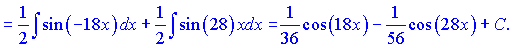
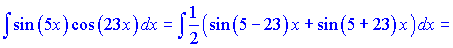
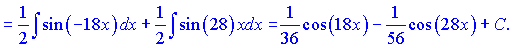
б) 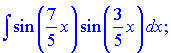
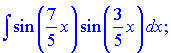
Розв'язок: За ІІІ формулою розписуємо добуток синусів через різницю косинусів, далі інтегруємо
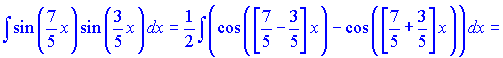
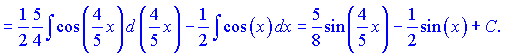
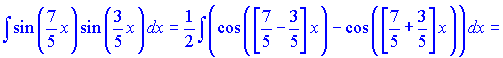
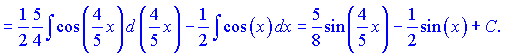
в) 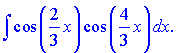
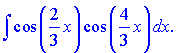
Розв'язок: За ІІ формулою розпишемо добуток синусів через різницю косинусів. Як інтегрувати косинус функцію детально описано на попередньому занятті.
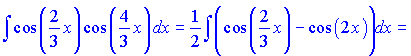
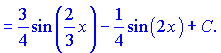
Методика розв'язування не складна і вимагає знання лише трьох тригонометричних формул, решта справи – знання табличних інтегралів для sin(k*x), cos(m*x). Практикуйте і не будете мати проблем з тригонометричними інтегралами.
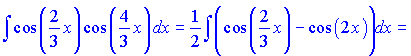
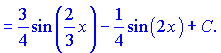
Методика розв'язування не складна і вимагає знання лише трьох тригонометричних формул, решта справи – знання табличних інтегралів для sin(k*x), cos(m*x). Практикуйте і не будете мати проблем з тригонометричними інтегралами.
Немає коментарів:
Дописати коментар