Геометричний зміст похідної. Дотична та нормаль до кривої
Значення похідної функції y=f(x) в точці x0 рівне кутовому коефіцієнту (тангенсу кута нахилу) дотичної, проведеної до графіка функції в точці з абсцисою x0
В цьому означенні і полягає геометричний зміст похідної.
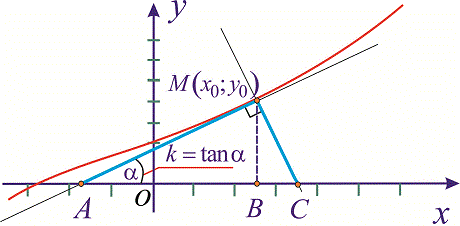
Нехай маємо рівняння кривої y=f(x) на площині та координати деякої точки M(x0;y0). Основними величинами, які можна знайти на основі цих даних є:
1) Рівняння дотичної до графіка функції
1) Рівняння дотичної до графіка функції
2) Рівняння нормалі
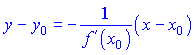
3) Довжина дотичної AM
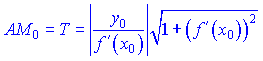
4) Довжина нормалі CM
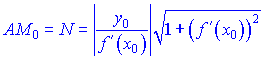
5) Довжина піддотичної AB
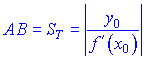
6) Довжина піднормалі BC
Виводити формули, які подані вище ми не будемо, оскільки це займе чимало часу, а Ви не запам'ятаєте цього. Лише нагадаємо, що піддотична – це проекція дотичної на вісь абсцис, а піднормаль - проекція нормалі на цю ж вісь. Розглянемо приклади зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика."
Приклад 1. (5.2.296) В яких точках кривої
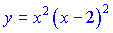
дотичні паралельні осі Ox?
дотичні паралельні осі Ox?
Розв'язок. Знайдемо кутовий коефіцієнт дотичної
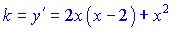
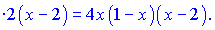
Щоб дотична була паралельна осі абсцис необхідно щоб кутовий коефіцієнт дотичної був рівний нулю. З цієї умови знаходимо шукані точки xi, а з рівняння кривої підстановкою xi знаходимо yi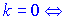
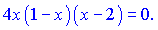
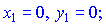
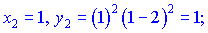
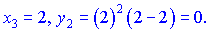
Задача розв'язана, координати точок дотику (0;0), (1;1), (2;0).
Щоб дотична була паралельна осі абсцис необхідно щоб кутовий коефіцієнт дотичної був рівний нулю. З цієї умови знаходимо шукані точки xi, а з рівняння кривої підстановкою xi знаходимо yi
Задача розв'язана, координати точок дотику (0;0), (1;1), (2;0).
Приклад 2. (5.2.307) Скласти рівняння дотичної і нормалі до параболи y=2x2 у точці A(1;2).
Розв'язок. Знайдемо кутовий коефіцієнт дотичної
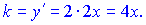
Підставляємо знайдене значення в формули дотичної та нормалі до кривої. В результаті отримаємо
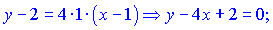
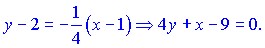
Рівняння дотичної 4y+x-9=0.
Підставляємо знайдене значення в формули дотичної та нормалі до кривої. В результаті отримаємо
Рівняння дотичної 4y+x-9=0.
Приклад 3. (5.2.314) Скласти рівняння нормалі до гіперболи
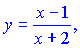
паралельної прямій 9x+3y+2=0.
паралельної прямій 9x+3y+2=0.
Розв'язок. Перепишемо рівняння нормалі, яке дане на початку статті, у вигляді
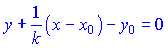
Знайдемо кутовий коефіцієнт дотичної
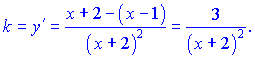
Поділимо рівняння паралельної прямої на три, щоб множники при одиниці в обох рівнянь були рівні
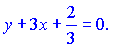
З умови паралельності прямих їх кутові коефіцієни мають бути рівні, звідси
1/k=3
Підставляємо знайдене вище значення k
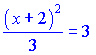
або
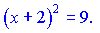
Розв'язками даного рівняння будуть точки
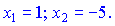
Підставимо їх у рівняння гіперболи і знайдемо ординати, які їм відповідають
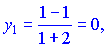
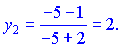
Таким чином, отримали точки (1; 0) та (5; 2). Підставивши їх в рівняння нормалі
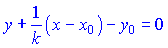
отримаємо рівняння
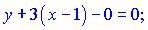
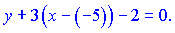
Розкривши дужки, матимемо шукані рівняння паралельних ліній
y+3x-3=0;
y+3x+13=0.
Якщо Ви отримаєте прямі з різними кутовими коефіцієнтами (числа при x) , то прямі вже не є паралельні, а Ви десь допустили помилку.
Знайдемо кутовий коефіцієнт дотичної
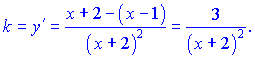
Поділимо рівняння паралельної прямої на три, щоб множники при одиниці в обох рівнянь були рівні
З умови паралельності прямих їх кутові коефіцієни мають бути рівні, звідси
1/k=3
Підставляємо знайдене вище значення k
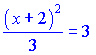
або
Розв'язками даного рівняння будуть точки
Підставимо їх у рівняння гіперболи і знайдемо ординати, які їм відповідають
Таким чином, отримали точки (1; 0) та (5; 2). Підставивши їх в рівняння нормалі
отримаємо рівняння
Розкривши дужки, матимемо шукані рівняння паралельних ліній
y+3x-3=0;
y+3x+13=0.
Якщо Ви отримаєте прямі з різними кутовими коефіцієнтами (числа при x) , то прямі вже не є паралельні, а Ви десь допустили помилку.
При розв'язуванні задач на дотичні та нормалі користуйтеся наведеними на початку уроку формулами, добре вникайте в суть умови завдання, правильно обчислюйте похідні.
Немає коментарів:
Дописати коментар