Інтеграли від добутку степеневих тригонометричних функцій sin^m(x). Правила пониження степеня
Дана тема стосується інтегрування тригонометричних виразів, які піднесені до певного степеня Такі інтеграли знаходять, понижуючи степінь підінтегральних функцій. При цьому існує три правила пониження степеня, які засновані на парності чи непарності показників.
Такі інтеграли знаходять, понижуючи степінь підінтегральних функцій. При цьому існує три правила пониження степеня, які засновані на парності чи непарності показників.
 Такі інтеграли знаходять, понижуючи степінь підінтегральних функцій. При цьому існує три правила пониження степеня, які засновані на парності чи непарності показників.
Такі інтеграли знаходять, понижуючи степінь підінтегральних функцій. При цьому існує три правила пониження степеня, які засновані на парності чи непарності показників.Правила пониження степеня
I. Якщо хоча б один з показників степеня підінтегральної функції є непарним числом, наприклад n=2k+1 то її можна перетворити за формулами:
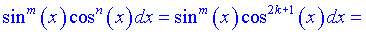
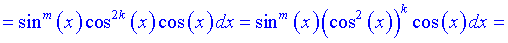
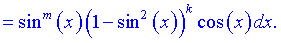 В таких випадках застосовують підстановку
В таких випадках застосовують підстановку При цьому вихідний інтеграл набуде вигляду
При цьому вихідний інтеграл набуде вигляду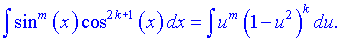 Питання зводиться до інтегрування суми степеневих функцій.
Питання зводиться до інтегрування суми степеневих функцій.
Якщо m=2k+1, то перетворення буде наступним
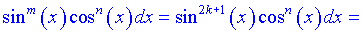
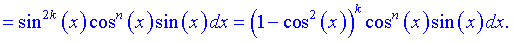 З вигляду бачимо, що заміна буде іншою
З вигляду бачимо, що заміна буде іншою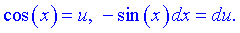 Початковий інтеграл запишеться у наступній формі
Початковий інтеграл запишеться у наступній формі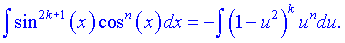 Знову отримуємо суму інтегралів.
Знову отримуємо суму інтегралів.
II. Якщо обидва показники – парні числа, то для пониження степеня використовують підстановку, яку запозичено із тригонометрії
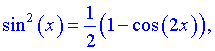
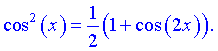 Застосування даних формул дозволяє понизити степінь підінтегральної функції, однак при великих значеннях степенів за даним правилом дещо більше обчислень ніж за першим.
Застосування даних формул дозволяє понизити степінь підінтегральної функції, однак при великих значеннях степенів за даним правилом дещо більше обчислень ніж за першим.
ІІІ. Показники непарні числа. У таких випадків використовують наступну тригонометричну рівність, щоб понизити степінь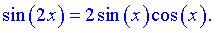 Подальше інтегрування зводиться до використання другого правила. Варто зазначити, що правило добре тим, що в підінтегральній функції отримуємо тільки парні аргументи
Подальше інтегрування зводиться до використання другого правила. Варто зазначити, що правило добре тим, що в підінтегральній функції отримуємо тільки парні аргументи
2x, 4x, 6x, ...
На цьому правила закінчуються і пора переходити до практичних обчислень.
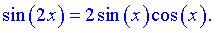 Подальше інтегрування зводиться до використання другого правила. Варто зазначити, що правило добре тим, що в підінтегральній функції отримуємо тільки парні аргументи
Подальше інтегрування зводиться до використання другого правила. Варто зазначити, що правило добре тим, що в підінтегральній функції отримуємо тільки парні аргументи2x, 4x, 6x, ...
На цьому правила закінчуються і пора переходити до практичних обчислень.
Приклад 1. Обчислити інтеграли
а) 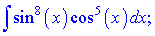
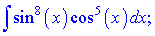
Розв'язок. Застосуємо до підінтегральної функції перше правило. При підстановці
sin(x)=u, cos(x)dx=du
підінтегральна функція набуде вигляду
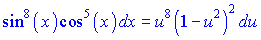
Проінтегруємо отриману функцію як поліном
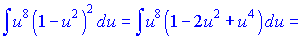
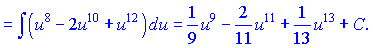
Повертаємося до використаної заміни змінних і міняємо назад u=sin(x). Інтеграл набуде кінцевого вигляду
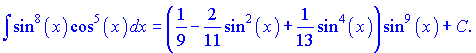
На цьому завдання розкрито всю силу методу пониження степеня.
sin(x)=u, cos(x)dx=du
підінтегральна функція набуде вигляду
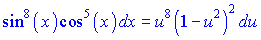
Проінтегруємо отриману функцію як поліном
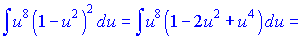
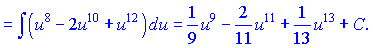
Повертаємося до використаної заміни змінних і міняємо назад u=sin(x). Інтеграл набуде кінцевого вигляду
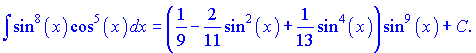
На цьому завдання розкрито всю силу методу пониження степеня.
б) 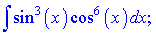
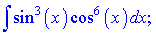
Розв'язок. До підінтегральної функції застосуємо заміну змінних
cos(x)=u, -sin(x)dx=du
і перетворюємо до наступного вигляду
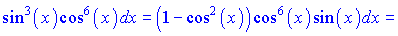
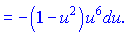
Проінтегрувати її зможе кожен студент, хто вивчив перші формули таблиці інтегралів
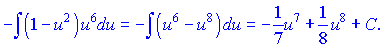
В попередніх змінних записуємо кінцеве значення інтегралу
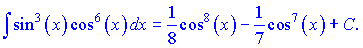
cos(x)=u, -sin(x)dx=du
і перетворюємо до наступного вигляду
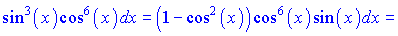
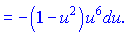
Проінтегрувати її зможе кожен студент, хто вивчив перші формули таблиці інтегралів
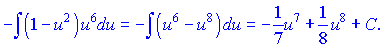
В попередніх змінних записуємо кінцеве значення інтегралу
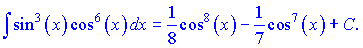
в) 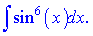
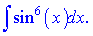
Розв'язок. Для цього інтегралу потрібно застосовувати друге правило. Перетворимо підінтегральну функцію, записавши синус в 6 степені через кубічну функцію від синуса
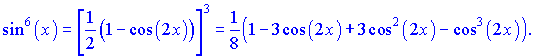
Проведемо інтегрування кожного з доданків
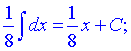
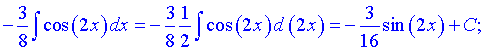
Квадрат косинуса понижаємо до 1 степеня та інтегруємо
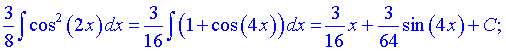
З косинусом в кубі маніпуляції дещо інші: розписуємо квадрат косинуса через основну формулу тригонометрії cos2(x)+sin2(x)=1.
Косинус, що залишився, вносимо під диференціал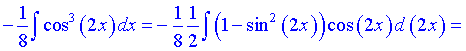
В результаті переходимо до нової змінної u=sin(2x) та інтегруємо квадратичну функцію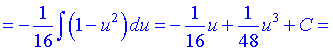
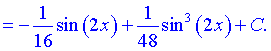
Підсумуємо доданки, попередньо згрупувавши подібні
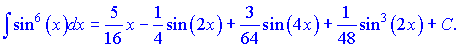
Подібних прикладів в інтернеті та літературі дуже багато. Правила пониження степеня для всіх залишаються однаковими, тому добре вивчіть в яких випадках їх застосовувати. Все інше зведеться до інтегрування, з яким у Вас при обчисленні не повинно виникати проблем.
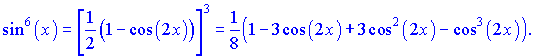
Проведемо інтегрування кожного з доданків
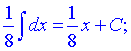
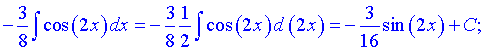
Квадрат косинуса понижаємо до 1 степеня та інтегруємо
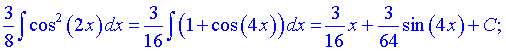
З косинусом в кубі маніпуляції дещо інші: розписуємо квадрат косинуса через основну формулу тригонометрії cos2(x)+sin2(x)=1.
Косинус, що залишився, вносимо під диференціал
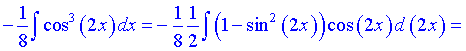
В результаті переходимо до нової змінної u=sin(2x) та інтегруємо квадратичну функцію
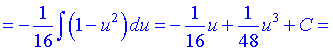
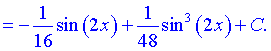
Підсумуємо доданки, попередньо згрупувавши подібні
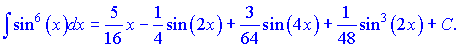
Подібних прикладів в інтернеті та літературі дуже багато. Правила пониження степеня для всіх залишаються однаковими, тому добре вивчіть в яких випадках їх застосовувати. Все інше зведеться до інтегрування, з яким у Вас при обчисленні не повинно виникати проблем.
Немає коментарів:
Дописати коментар