Границя функції в точці — фундаментальне поняття математичного аналізу, зокрема аналізу функцій дійсної змінної, число, до якого прямує значення функції, якщо її аргумент прямує до заданої точки. Строге математичне означення границі функції дається мовою δ-ε.
Означення[1]
Означення за Коші
Нехай , — гранична точка множини A. Число a називається границею функції у точці , якщо
Позначення:
або
- при
Означення за Гейне: Якщо для довільної послідовності точок взятої з області визначення функції відповідна послідовність значень функції збігається до того самого числа, то це число називають границею функції в точці.
Односторонні границі
Одностороння границя — це границя функції однієї змінної в деякій точці, коли аргумент прямує до значення аргументу у цій точці окремо зі сторони більших аргументів (правостороння границя), або зі сторони менших аргументів (лівостороння границя). Тобто, є сенс говорити про односторонні границі функції у деякій точці тільки тоді, коли у цій точці лівостороння границя функції не дорівнює правосторонній.
- Правосторонню границю прийнято позначати наступним чином:
- Для лівосторонньої границі прийняті такі позначення:
- Використовуються також наступні скорочення:
- і для правої границі;
- і для лівої границі.
Перша та друга визначні границі. Приклади
Приклади границь, що містять невизначеності виду нуль розділити на нуль (0/0) часто зустрічаються у тригонометричних функціях. Для їх розкриття використовують першу чудову (особливу) границю, суть якої полягає в тому, що границя відношення синус функції до аргументу, коли той прямує до нуля рівна одиниці
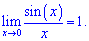
На її основі можна отримати ряд корисних для практики наслідків першої границі
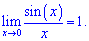
На її основі можна отримати ряд корисних для практики наслідків першої границі
1) 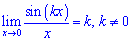
2)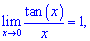
3)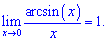
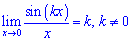
2)
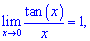
3)
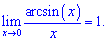
Друга особлива границя дозволяє розкривати невизначеності виду одиниця в степені безмежність 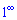 .
.
Формуа другої чудової границя аведена нижче
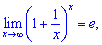
де e=2,71828182849045... – експонента.
На основі другої особливої границі отримують наступні формули (висновки)
1)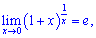
2)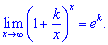
Завдання на границі, які зводяться до першої та другої особливих (чудових) границь зустрічаються доволі рідко, однак без наведених формул такі приклади не розв'язати. Розглянемо деякі приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика", що приводять до застосування особливих границь.
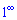 .
.Формуа другої чудової границя аведена нижче
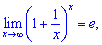
де e=2,71828182849045... – експонента.
На основі другої особливої границі отримують наступні формули (висновки)
1)
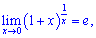
2)
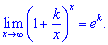
Завдання на границі, які зводяться до першої та другої особливих (чудових) границь зустрічаються доволі рідко, однак без наведених формул такі приклади не розв'язати. Розглянемо деякі приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика", що приводять до застосування особливих границь.
Приклад 1. Знайти границю фунціїй.
1) (4. 388)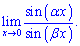
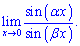
Розв'язок. Помножимо чисельник і знаменник на аргумент та зведемо до першої чудової границі
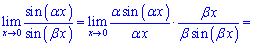
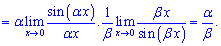
Для одних це легко побачити, іншим важко зрозуіти схему обчислень. А її суть в отриманні запису sin(x)/x, все що буде при цьому множником і буде складати границю функції.
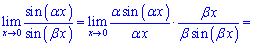
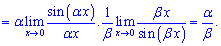
Для одних це легко побачити, іншим важко зрозуіти схему обчислень. А її суть в отриманні запису sin(x)/x, все що буде при цьому множником і буде складати границю функції.
2) (4. 393)

Розв'язок. Поділимо чисельник і знаменник на змінну x. В результаті і там і там отримаємо "число" + наслідок перої особливої границі
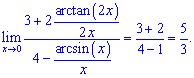
Настільки легко можна обчислювати, якщо мати шпаргалку та знати, що потрібно шукати.
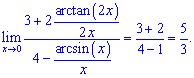
Настільки легко можна обчислювати, якщо мати шпаргалку та знати, що потрібно шукати.
3) (4. 399)

Розв'язок.Згідно формули розвинення кореня в околі одиниці в ряд
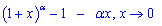
знаменник дробу можна перетворити наступним чином
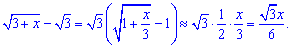
На основі цього знаходимо границю функції
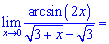
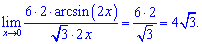
В чисельнику фігурував арксинус подвійного аргументу, тому для зведення під правило першої границі подвійний аргумент виділяємо також в знаменнику. Далі виписуємо границю у вигляді ірраціонального числа та, домноженням чисельника і знаменника на корінь з 3, приводимо запис до коректного вигляду.
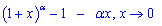
знаменник дробу можна перетворити наступним чином
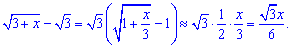
На основі цього знаходимо границю функції
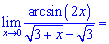
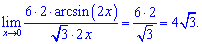
В чисельнику фігурував арксинус подвійного аргументу, тому для зведення під правило першої границі подвійний аргумент виділяємо також в знаменнику. Далі виписуємо границю у вигляді ірраціонального числа та, домноженням чисельника і знаменника на корінь з 3, приводимо запис до коректного вигляду.
4) (4. 432)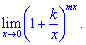
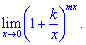
Розв'язок.Зведемо показникову функцію під правило другої визначної границі. Для цього в степені утворємо множник обернено пропорційний до доданку в дужках.
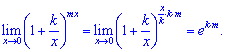
Все що залишиться і буде степенем експоненти. Застосовуйте цю властивість показників у подібних завданнях на границі.
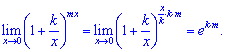
Все що залишиться і буде степенем експоненти. Застосовуйте цю властивість показників у подібних завданнях на границі.
5) (4. 437)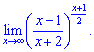
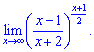
Розв'язок. В такого роду завданнях функцію слід звести під формулу другої визначної границі.
Для цього зведемо до правильного дробу вираз в дужках
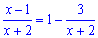
та підставимо в границю. Після розділення показників отримаємо добуток двох границь
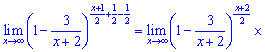
Для цього зведемо до правильного дробу вираз в дужках
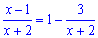
та підставимо в границю. Після розділення показників отримаємо добуток двох границь
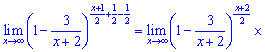
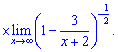
Спростимо перший множник
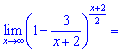
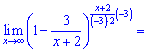
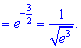
Друга границя рівна одиниці
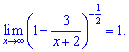
Просьба не вважати її чимось схожим на другу границю, в показнику немає аргументу "х", а вираз в дужках прямує до одиниці.
В результаті множення отримаємо
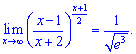
6) 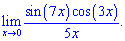
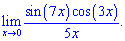
Розв'язок. Зведемо до першої визначної границі.
Тут зразу можна здогадатися, що косинус ніякого вкладу не внесе, оскільки в нулі рівний одиниці. Залишається в знаменнику отримати 7x
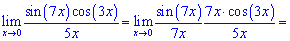
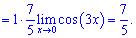
Після незначних перетворень границя функції рівна 7/5.
Тут зразу можна здогадатися, що косинус ніякого вкладу не внесе, оскільки в нулі рівний одиниці. Залишається в знаменнику отримати 7x
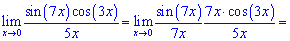
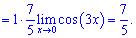
Після незначних перетворень границя функції рівна 7/5.
7) 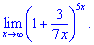
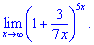
Розв'язок. Перетворимо показник для того, щоб можна було застосувати другу визначну границю.
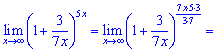
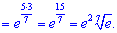
Перетворення дробу в показнику не складне і в результаті обчислень отримаємо e15/7.
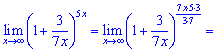
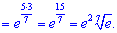
Перетворення дробу в показнику не складне і в результаті обчислень отримаємо e15/7.
Подібних прикладів можна навести сотні. Їх розв'язування дозволить закріпити Вам кращі практичні навички, тож пробуйте розв'язувати самостійно. Якщо в навчанні Вам зустрінуться важкі границі, порахувати які Ви не в змозі,
Теорія границь - один з розділів математичного аналізу, який одним під силу освоїти, інші з труднощами обчислюють границі. Питання знаходження границь є досить загальним, оскільки існують десятки прийомів рішення границь різних видів. Одні і ті ж границі можна знайти як за правилом Лопіталя, так і без нього. Буває, що розклад в ряд нескінченно малих функцій дозволяє швидко отримати потрібний результат. Існує набір прийомів і хитрощів, що дозволяють знайти границю функції будь-якої складності. В даній статті спробуємо розібратися в основних типах границь, які найбільш часто зустрічаються на практиці. Теорію та означення границі ми тут давати не будемо, в інтернеті безліч ресурсів де це розжовано. Тому займемося практичним обчисленням, саме тут у Вас і починається "не знаю! не вмію! нас не вчили!"
Обчислення границь методом підстановки
Приклад 1. Знайти границю функції
Lim((x2-3*x)/(2*x+5), x=3).
Розв'язання: Такого сорту приклади обчислюють звичайною підстановкою
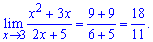
Границя рівна 18/11.
Нічого складного і мудрого в таких границях немає, підставили значення, обчислили, записали границю у відповідь. Зате на базі таких границь всіх привчають, що перш за все потрібно підставити значення у функцію (принаймі перевірити, що отримаємо? чи - до чого прямує?).
Далі границі ускладнюють, вводять поняття безмежності, невизначеності і т.д.
Lim((x2-3*x)/(2*x+5), x=3).
Розв'язання: Такого сорту приклади обчислюють звичайною підстановкою
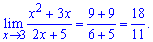
Границя рівна 18/11.
Нічого складного і мудрого в таких границях немає, підставили значення, обчислили, записали границю у відповідь. Зате на базі таких границь всіх привчають, що перш за все потрібно підставити значення у функцію (принаймі перевірити, що отримаємо? чи - до чого прямує?).
Далі границі ускладнюють, вводять поняття безмежності, невизначеності і т.д.
Границі з невизначеністю типу безмежність розділити на безмежність. Методи розкриття невизначеності
Приклад 2. Знайти границю функції
Lim((x2+2x)/(4x^2+3x-4), x=infinity).
Розв'язання: Задана границя типу поліном розділити на поліном, причому змінна прямує до безмежності
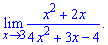
Проста підстановка значення до якого прямує змінна знайти границю не допоможе, отримаємо невизначеність виду безмежність розділити на безмежність.
Алгоритм обчислення границі полягає у знаходженні найбільшого степеня "ікс" в чисельнику чи знаменнику. Далі на нього спрощують чисельник і знаменник і знаходять границю
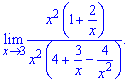
Оскільки значення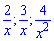 прямують до нуля при змінній прямуючій до безмежності то ними нехтують, або записують в кінцевий вираз у вигляді нулів
прямують до нуля при змінній прямуючій до безмежності то ними нехтують, або записують в кінцевий вираз у вигляді нулів
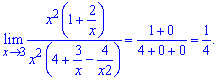
Зразу з практики можна отримати два висновки, які є підказкою в обчисленнях. Якщо змінна прямує до безмежності і степінь чисельника більший від степені знаменника то границя рівна безмежності. В протилежному випадку, якщо поліном в знаменнику старшого порядку ніж в чисельнику границя рівна нулю.
Формулами границі можна записати так
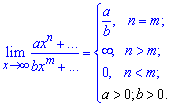
Якщо маємо в границі звичайний поліном без дробів, то границя теж рівна безмежності
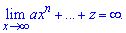
Наступний тип границь стосується поведінки функцій біля нуля.
Lim((x2+2x)/(4x^2+3x-4), x=infinity).
Розв'язання: Задана границя типу поліном розділити на поліном, причому змінна прямує до безмежності
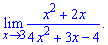
Проста підстановка значення до якого прямує змінна знайти границю не допоможе, отримаємо невизначеність виду безмежність розділити на безмежність.
Алгоритм обчислення границі полягає у знаходженні найбільшого степеня "ікс" в чисельнику чи знаменнику. Далі на нього спрощують чисельник і знаменник і знаходять границю
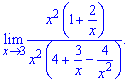
Оскільки значення
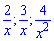 прямують до нуля при змінній прямуючій до безмежності то ними нехтують, або записують в кінцевий вираз у вигляді нулів
прямують до нуля при змінній прямуючій до безмежності то ними нехтують, або записують в кінцевий вираз у вигляді нулів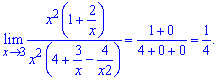
Зразу з практики можна отримати два висновки, які є підказкою в обчисленнях. Якщо змінна прямує до безмежності і степінь чисельника більший від степені знаменника то границя рівна безмежності. В протилежному випадку, якщо поліном в знаменнику старшого порядку ніж в чисельнику границя рівна нулю.
Формулами границі можна записати так
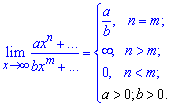
Якщо маємо в границі звичайний поліном без дробів, то границя теж рівна безмежності
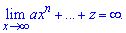
Наступний тип границь стосується поведінки функцій біля нуля.
Приклад 3. Знайти границю функції
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Розв'язання: Тут вже виносити найстарший доданок полінома не потрібно. З точністю до навпаки, необхідно знайти найменший степінь чисельника і знаменника та обчислити границю
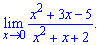
Значення x^2; x прямують до нуля коли змінна прямує до нуля Тому ними нехтують, таким чином отримаємо
Тому ними нехтують, таким чином отримаємо
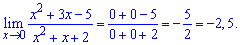
Границя рівна 2,5.
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Розв'язання: Тут вже виносити найстарший доданок полінома не потрібно. З точністю до навпаки, необхідно знайти найменший степінь чисельника і знаменника та обчислити границю
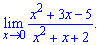
Значення x^2; x прямують до нуля коли змінна прямує до нуля
 Тому ними нехтують, таким чином отримаємо
Тому ними нехтують, таким чином отримаємо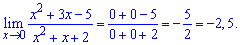
Границя рівна 2,5.
Границі з невизначеністю типу 0/0 і методи їх обчислень
Зразу всі згадують правило, що ділити на нуль не можна. Однак в цьому контексті маємо на увазі нескінченно малі функції.
Розглянемо для наочності приклад
Розглянемо для наочності приклад
Приклад 4. Знайти границю функції
Lim((3x^2+10x+7)/(x+1), x=-1).
Розв'язання: При підстановці у знаменник x=-1 отримаємо нуль, те ж саме отримаємо в чисельнику. Отже маємо невизначеність типу 0/0.
Боротися з такою невизначеністю просто: потрібно розкласти поліном на множники, а точніше виділити множник, який перетворює все на нуль.
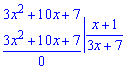
Отже, границю можна записати у вигляді
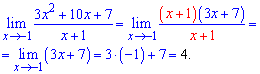
Ось і вся методика. Так само поступаємо, якщо маємо границі виду многочлен розділити на многочлен.
Lim((3x^2+10x+7)/(x+1), x=-1).
Розв'язання: При підстановці у знаменник x=-1 отримаємо нуль, те ж саме отримаємо в чисельнику. Отже маємо невизначеність типу 0/0.
Боротися з такою невизначеністю просто: потрібно розкласти поліном на множники, а точніше виділити множник, який перетворює все на нуль.
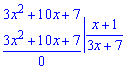
Отже, границю можна записати у вигляді
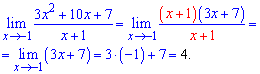
Ось і вся методика. Так само поступаємо, якщо маємо границі виду многочлен розділити на многочлен.
Приклад 5. Знайти границю функції
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Розв'язання: Пряма підстановка показує
2*4-7*2+6=0;
3*4-2-10=0
що маємо невизначеність типу 0/0.
Поділимо поліноми на множник, що дає особливість
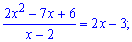
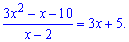
Є практики, які вчать, що поліноми 2 порядку тобто вигляду "квадратні рівняння" слід розв'язувати через дискримінант. Але моя практика показує, що це довше і заплутаніше, тому позбувайтеся особливості у границі за вказаним алгоритмом. Таким чином записуємо поліноми у вигляді простих множників та підставляємо у границю
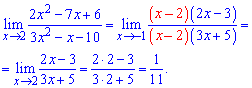
Як бачите, нічого складного в обчисленні таких границь немає. Ділити многочлени Ви на момент вивчення границь вмієте, принаймні за програмою мали вже пройти. Серед завдань на невизначеність типу 0/0 зустрічаються такі, в яких потрібно застосовувати формули скороченого множення. Але якщо Ви їх не знаєте, то діленням многочлена на одночлен можна отримати потрібну формулу
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Розв'язання: Пряма підстановка показує
2*4-7*2+6=0;
3*4-2-10=0
що маємо невизначеність типу 0/0.
Поділимо поліноми на множник, що дає особливість
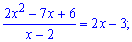
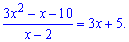
Є практики, які вчать, що поліноми 2 порядку тобто вигляду "квадратні рівняння" слід розв'язувати через дискримінант. Але моя практика показує, що це довше і заплутаніше, тому позбувайтеся особливості у границі за вказаним алгоритмом. Таким чином записуємо поліноми у вигляді простих множників та підставляємо у границю
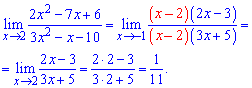
Як бачите, нічого складного в обчисленні таких границь немає. Ділити многочлени Ви на момент вивчення границь вмієте, принаймні за програмою мали вже пройти. Серед завдань на невизначеність типу 0/0 зустрічаються такі, в яких потрібно застосовувати формули скороченого множення. Але якщо Ви їх не знаєте, то діленням многочлена на одночлен можна отримати потрібну формулу
Приклад 6. Знайти границю функції
Lim((x^2-9)/(x-3), x=3).
Розв'язання: Маємо невизначеність типу 0/0. В чисельнику застосовуємо формулу скороченого множення
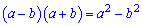
і обчислюємо потрібну границю
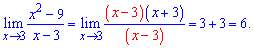
В результаті розкриємо ірраціональність та отримаємо 6.
Lim((x^2-9)/(x-3), x=3).
Розв'язання: Маємо невизначеність типу 0/0. В чисельнику застосовуємо формулу скороченого множення
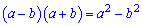
і обчислюємо потрібну границю
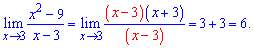
В результаті розкриємо ірраціональність та отримаємо 6.
Метод розкриття невизначеності множенням на спряжене
Метод застосовують до границь, в яких невизначеність породжують ірраціональні функції. Чисельник або знаменник перетворюється в точці знаходження границі в нуль і невідомо як знайти границю.
Приклад 7. Знайти границю функції
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).Розв'язання: Подамо границю у вигляді формули
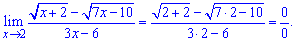
При підставленні значення отримаємо невизначеність типу 0/0.
Схема обходу даної особливості полягає у множенні ірраціональності на спряжене. Щоб вираз не змінився знаменник потрібно поділити на таке ж значення
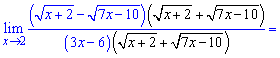
За правилом різниці квадратів спрощуємо чисельник та обчислюємо границю
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).Розв'язання: Подамо границю у вигляді формули
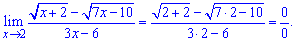
При підставленні значення отримаємо невизначеність типу 0/0.
Схема обходу даної особливості полягає у множенні ірраціональності на спряжене. Щоб вираз не змінився знаменник потрібно поділити на таке ж значення
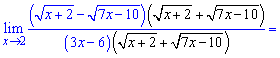
За правилом різниці квадратів спрощуємо чисельник та обчислюємо границю
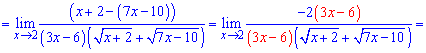
Спрощуємо доданки, що створюють особливість в границі та виконуємо підстановку
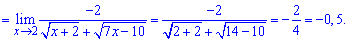
Вкінці залишиться обчислити орені в знаменнику та спротити дріб.
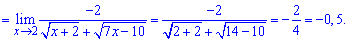
Вкінці залишиться обчислити орені в знаменнику та спротити дріб.
Приклад 8. Знайти границю функції
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).Розв'язання: Границя має особливість виду 0/0.
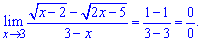
Для розкриття множимо і ділимо на спряжене
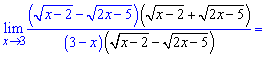
Записуємо різницю квадратів
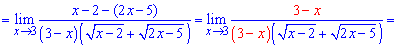
Спрощуємо доданки, що вносять особливість та знаходимо границю
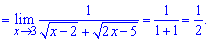
Досить гарний прикад на позбуття особливості методом розкриття ірраціональності.
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).Розв'язання: Границя має особливість виду 0/0.
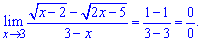
Для розкриття множимо і ділимо на спряжене
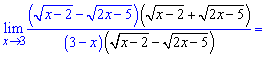
Записуємо різницю квадратів
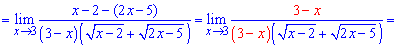
Спрощуємо доданки, що вносять особливість та знаходимо границю
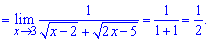
Досить гарний прикад на позбуття особливості методом розкриття ірраціональності.
Приклад 9. Знайти границю функції
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Розв'язання: Підставимо двійку в границю.
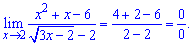
Отримаємо невизначеність 0/0.
Знаменник потрібно помножити на спряжений вираз, а в чисельнику розв'язати квадратне рівняння. Оскільки відомо, що 2 є коренем, то другий корінь знаходимо з теореми Вієта
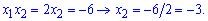
Таким чином чисельник запишемо у вигляді
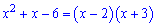
та підставимо у границю
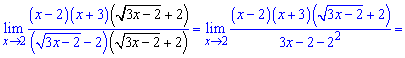
Звівши різницю квадратів позбуваємося особливості в чисельнику і знаменнику
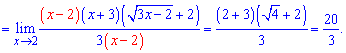
Наведеним чином можна позбутися особливості в багатьох прикладах, а застосування треба помічати скрізь, де задано різницю коренів, що перетворюється в нуль при підстановці. Інші типи границь стосуються показникових функцій, нескінченно малих функцій, логарифмів, особливих границь і інших методик. Але про це Ви зможете прочитати в наведених далі статтях про границі.
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Розв'язання: Підставимо двійку в границю.
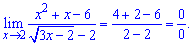
Отримаємо невизначеність 0/0.
Знаменник потрібно помножити на спряжений вираз, а в чисельнику розв'язати квадратне рівняння. Оскільки відомо, що 2 є коренем, то другий корінь знаходимо з теореми Вієта
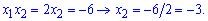
Таким чином чисельник запишемо у вигляді
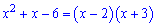
та підставимо у границю
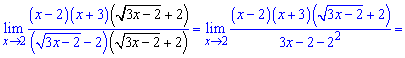
Звівши різницю квадратів позбуваємося особливості в чисельнику і знаменнику
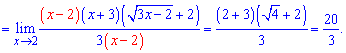
Наведеним чином можна позбутися особливості в багатьох прикладах, а застосування треба помічати скрізь, де задано різницю коренів, що перетворюється в нуль при підстановці. Інші типи границь стосуються показникових функцій, нескінченно малих функцій, логарифмів, особливих границь і інших методик. Але про це Ви зможете прочитати в наведених далі статтях про границі.
Обчислення границь в Мейплі
Даний матеріал корисний перш за все для студентів. Можливо в програмі навчання, а дехто для себе вивчає математичні програми для полегшення навчання і перевірки розв'язків. Це можуть бути математичні пакети MathСad, Мathematica, Maple. Обчислення границь в Мейплі досить просто організувати навіть новачку. Все, що потрібно - правильно ввести функцію, границю якої знаходимо.
Знаходження границь за правилом Лопіталя
Ефективним способом знаходження границь функцій, які мають особливості типу безмежність розділити на безмежність 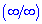 чи нуль розділити на нуль (0/0) є застосування правила Лопіталя: границя відношення двох нескінченно малих або двох нескінченно великих функцій рівна границі відношення їх похідних, якщо такі існують
чи нуль розділити на нуль (0/0) є застосування правила Лопіталя: границя відношення двох нескінченно малих або двох нескінченно великих функцій рівна границі відношення їх похідних, якщо такі існують
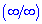 чи нуль розділити на нуль (0/0) є застосування правила Лопіталя: границя відношення двох нескінченно малих або двох нескінченно великих функцій рівна границі відношення їх похідних, якщо такі існують
чи нуль розділити на нуль (0/0) є застосування правила Лопіталя: границя відношення двох нескінченно малих або двох нескінченно великих функцій рівна границі відношення їх похідних, якщо такі існують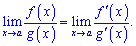
Розкриття невизначеностей виду нескінченність мінус нескінченність, нуль помножити на нескінченність, нуль в степені нескінченність або навпаки 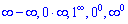 зводиться попередньо до розглянутих вище невизначеностей (правила Лопіталя). Якщо одна функція прямує до нуля
зводиться попередньо до розглянутих вище невизначеностей (правила Лопіталя). Якщо одна функція прямує до нуля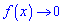 , а друга до безмежності
, а друга до безмежності 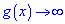 при змінній прямуючій до певного значення
при змінній прямуючій до певного значення  , то для застосування правила Лопіталя необхідно виконати наступні перетворення
, то для застосування правила Лопіталя необхідно виконати наступні перетворення
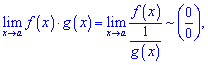
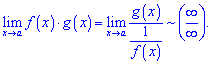
У випадку трьох останніх невизначеностей (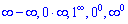 ) потрібно застосовувати перетворення
) потрібно застосовувати перетворення
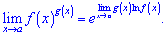
Розглянемо деякі приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" на застосування правила Лопіталя.
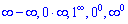 зводиться попередньо до розглянутих вище невизначеностей (правила Лопіталя). Якщо одна функція прямує до нуля
зводиться попередньо до розглянутих вище невизначеностей (правила Лопіталя). Якщо одна функція прямує до нуля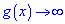 при змінній прямуючій до певного значення
при змінній прямуючій до певного значення  , то для застосування правила Лопіталя необхідно виконати наступні перетворення
, то для застосування правила Лопіталя необхідно виконати наступні перетворення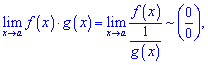
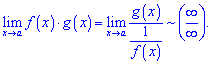
У випадку трьох останніх невизначеностей (
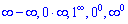 ) потрібно застосовувати перетворення
) потрібно застосовувати перетворення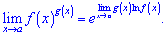
Розглянемо деякі приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" на застосування правила Лопіталя.
Приклад 1. Знайти границі.
1) (5. 626)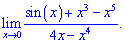
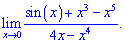
Розв'язок. Підстановкою встановлюємо, що маємо невизначеність виду нуль на нуль (0/0). Щоб її позбутися застосуємо правило Лопіталя
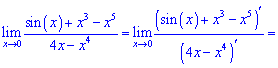
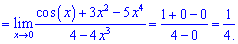
Границя функції рівна 1/4.
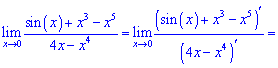
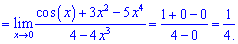
Границя функції рівна 1/4.
2) (6. 629)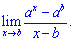
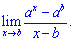
Розв'язок. Як і у попередньому прикладі маємо невизначеність (0/0). За правилом Лопіталя обчислюємо похідну окремо чисельника і знаменника
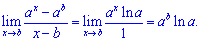
Другий доданок в чисельнику є сталою, тому його похідна рівна нулю.
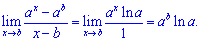
Другий доданок в чисельнику є сталою, тому його похідна рівна нулю.
3) (6. 634)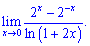
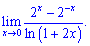
Розв'язок. Враховуючи особливість (0/0) застосовуємо формулу Лопіталя
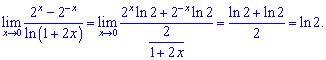
Показникові функції в нулю рівні одиниці, тому залишаться тільки логарифми.
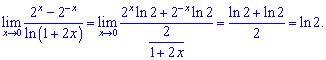
Показникові функції в нулю рівні одиниці, тому залишаться тільки логарифми.
4) (4. 639)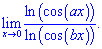
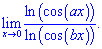
Розв'язок. Розкриваємо невизначеність виду (0/0)
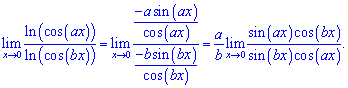
Чисельник та знаменник перетворимо до суми синусів на основі правила добутку
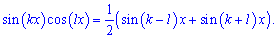
В результаті запишемо чисельник і знаменник через формули
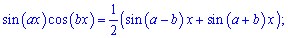
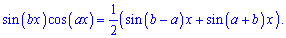
Підставимо знайдені значення в границю
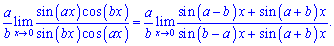
Знову отримали особливість 0/0, тому повторно застосовуємо правило Лопіталя
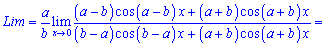
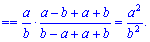
Похідна від синуса рівна косинусу, ну і осільки маємо складену функцію то множимо на похідну від залежності під синусом. При граничному переході враховано, що косинус функція прямує до одиниці при змінній, що прямує до нуля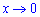 .
.
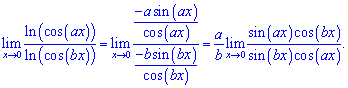
Чисельник та знаменник перетворимо до суми синусів на основі правила добутку
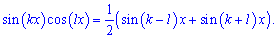
В результаті запишемо чисельник і знаменник через формули
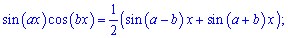
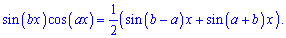
Підставимо знайдені значення в границю
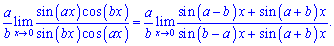
Знову отримали особливість 0/0, тому повторно застосовуємо правило Лопіталя
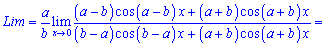
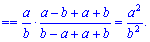
Похідна від синуса рівна косинусу, ну і осільки маємо складену функцію то множимо на похідну від залежності під синусом. При граничному переході враховано, що косинус функція прямує до одиниці при змінній, що прямує до нуля
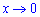 .
.
5) (4. 645)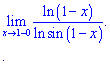
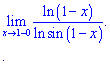
Розв'язок. Маємо особливість виду безмежність розділити на безмежність 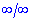 .
.
Знайдемо похідні логарифмів
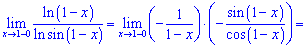
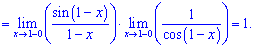
Після підстановки отримаємо дві функції, одну з яких знаходимо через першу чудову границю.
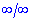 .
.Знайдемо похідні логарифмів
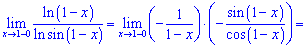
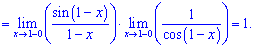
Після підстановки отримаємо дві функції, одну з яких знаходимо через першу чудову границю.
6) (4. 668)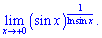
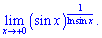
Розв'язок. Зводимо функцію під формулу другої чудової границі
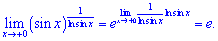
Отримали у результаті обчислень експоненту.
Застосування правила Лопіталя показало переваги знаходження границі при розкритті невизначеностей. Користуйтеся формулою Лопіталя на практиці і Вам не буде важко знаходити подібні границі у навчанні.
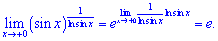
Отримали у результаті обчислень експоненту.
Застосування правила Лопіталя показало переваги знаходження границі при розкритті невизначеностей. Користуйтеся формулою Лопіталя на практиці і Вам не буде важко знаходити подібні границі у навчанні.
 ,
,  —
—  у точці
у точці 

 при
при 


 і
і  для правої границі;
для правої границі; і
і  для лівої границі.
для лівої границі.
Немає коментарів:
Дописати коментар