Поверхневий інтеграл ІІ роду
Знаходження поверхневого інтегралу другого роду полягає в обчисленні подвійних інтегралів по орієнтованих поверхнях від наперед заданих функцій. Теорія подвійних інтегралів детально розписана в підручниках та методичках, більше труднощів виникає у студентів із самим інтегруванням, вірніше з переходом до подвійних, правильним знаходженням меж інтегрування. Самі на ці питання Ви можете знайти відповіді, переглянувши готові відповіді до практикуму з вищої математики.
ЗАВДАННЯ 6.2 Обчислити поверхневий інтеграл int(x*dy*dz+y*dx*dz+z*dx*dy,ds) по поверхні сігма – зовнішня сторона куба, обмеженого площинами z=0, y=0, x=0, x=1, y=1, z=1.

Розв'язання: Побудуємо куб, що обмежений заданими площинами:
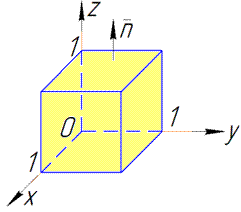
Обчислюємо поверхневий інтеграл ІІ роду по всім шести поверхням, тому формула прийме вигляд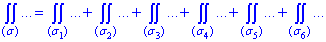
Для кожної поверхні куба запишемо рівняння площини і її межі по гранях:
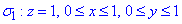 звідси
звідси 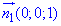 - нормальний зовнішній вектор.
- нормальний зовнішній вектор.
На площини Oxz і Oyz поверхня z=1 проектується в прямі, де dydz=0, dxdz=0
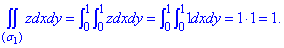
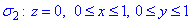 звідси вектор нормалі рівний
звідси вектор нормалі рівний 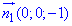
На площини Oxz і Oyz поверхня z=0 проектується в прямі, де dydz=0.
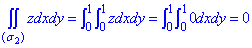
Оскільки в умові куб обмежений площинами z=0, y=0, x=0, x=1, y=1, z=1, то по відповідних площинах ситуація буде аналогічна і тому поверхневий інтеграл рівний сумі
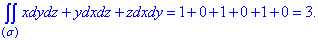

Розв'язання: Побудуємо куб, що обмежений заданими площинами:

Обчислюємо поверхневий інтеграл ІІ роду по всім шести поверхням, тому формула прийме вигляд
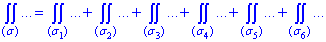
Для кожної поверхні куба запишемо рівняння площини і її межі по гранях:
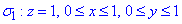 звідси
звідси 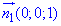 - нормальний зовнішній вектор.
- нормальний зовнішній вектор.На площини Oxz і Oyz поверхня z=1 проектується в прямі, де dydz=0, dxdz=0
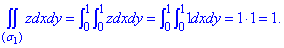
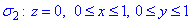 звідси вектор нормалі рівний
звідси вектор нормалі рівний 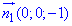
На площини Oxz і Oyz поверхня z=0 проектується в прямі, де dydz=0.
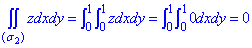
Оскільки в умові куб обмежений площинами z=0, y=0, x=0, x=1, y=1, z=1, то по відповідних площинах ситуація буде аналогічна і тому поверхневий інтеграл рівний сумі
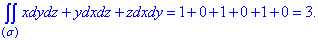
ЗАВДАННЯ 6.4 Обчислити потік векторного поля 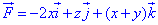 через замкнену поверхню
через замкнену поверхню 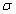 :
:
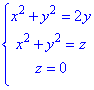
(нормаль зовнішня).
Розв'язання:Рівняння x^2+y^2=2y зводимо до канонічного вигляду x^2+(y-1)^2=1 - коловий циліндр, що витягнутий вздовж осі Oz і радіусом R=1; z=x^2+y^2 - еліптичний параболоїд з вершиною (0;0;0) вітками витягнутий вгору вздовж осі Oz. Побудуємо циліндр та параболоїд
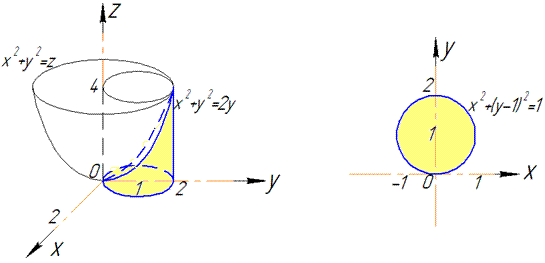
Це вносить певну ясність в умову завдання та й Вам приємніше читати відповіді з малюнками, ніж голі формули.
Як бачимо з рисунку половина області V задається наступними межами:
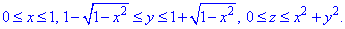
Розглядаємо половини в силу парності всіх функцій, тому інцевий результат помножимо на 2.
Обчислимо дивергенцію векторного поля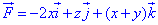 :
: 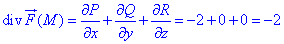
де P=P(x;y;z)=-2x, Q=Q(x;y;z)=z, R=R(x;y;z)=x+y множники при напрямних векторного поля.
Знайдемо потік векторного поля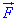 за формулою Остроградського-Гаусса:
за формулою Остроградського-Гаусса:
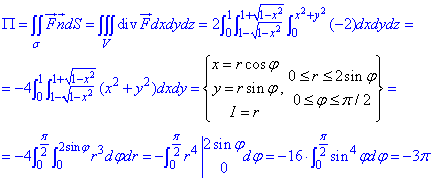
Потрійний інтеграл зводимо до подвійного, а дальше, перейшовши до полярної системи координат, знаходимо значення інтегралу.
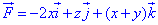 через замкнену поверхню
через замкнену поверхню 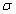 :
: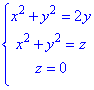
(нормаль зовнішня).
Розв'язання:Рівняння x^2+y^2=2y зводимо до канонічного вигляду x^2+(y-1)^2=1 - коловий циліндр, що витягнутий вздовж осі Oz і радіусом R=1; z=x^2+y^2 - еліптичний параболоїд з вершиною (0;0;0) вітками витягнутий вгору вздовж осі Oz. Побудуємо циліндр та параболоїд
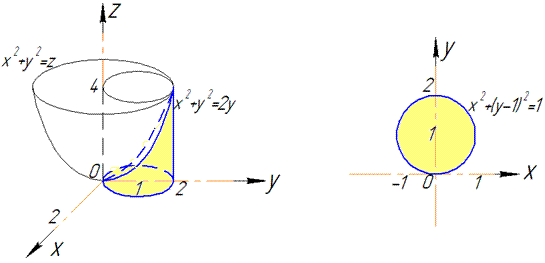
Це вносить певну ясність в умову завдання та й Вам приємніше читати відповіді з малюнками, ніж голі формули.
Як бачимо з рисунку половина області V задається наступними межами:
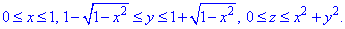
Розглядаємо половини в силу парності всіх функцій, тому інцевий результат помножимо на 2.
Обчислимо дивергенцію векторного поля
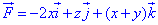 :
: 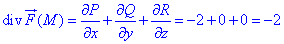
де P=P(x;y;z)=-2x, Q=Q(x;y;z)=z, R=R(x;y;z)=x+y множники при напрямних векторного поля.
Знайдемо потік векторного поля
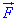 за формулою Остроградського-Гаусса:
за формулою Остроградського-Гаусса: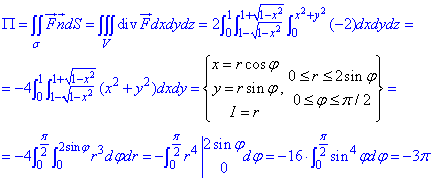
Потрійний інтеграл зводимо до подвійного, а дальше, перейшовши до полярної системи координат, знаходимо значення інтегралу.
ЗАВДАННЯ 6.6 Обчислити поверхневий інтеграл int(z2*dy*dz,ds) по поверхні сігма, де  – зовнішня частина еліпсоїда
– зовнішня частина еліпсоїда 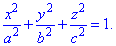
Розв'язання: Побудуємо еліпсоїд та його проекцію в декартову пощину:
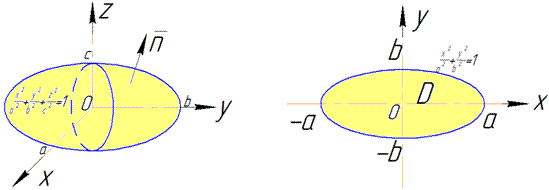
Проекція площини на Oxy обмежена наступним чином
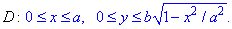
(Взяли чверть області).Далі виражаємо поверхню як функцію z(x,y)
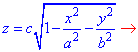
z^2=(1-x^2/a^2-y^2/b^2)*c^2та знаходимо диференціал поверхні за формулою
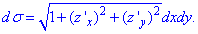
Цей інтеграл будемо обчислювати для верхньої половини еліпсоїда, оскільки для нижньої значення поверхневого інтеграла буде таким же. Таким чином, результат помножимо на 2.
Обчислимо направляючі косинуси заданої поверхні:
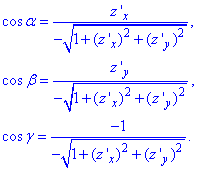
Перед радикалами поставимо знак « – », оскільки нормаль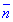 зовнішня утворює з віссю Oz гострий кут. Отже зводимо поверхневий інтеграл до повторного, далі робимо заміну змінних та знаходимо якобіан переходу.
зовнішня утворює з віссю Oz гострий кут. Отже зводимо поверхневий інтеграл до повторного, далі робимо заміну змінних та знаходимо якобіан переходу.
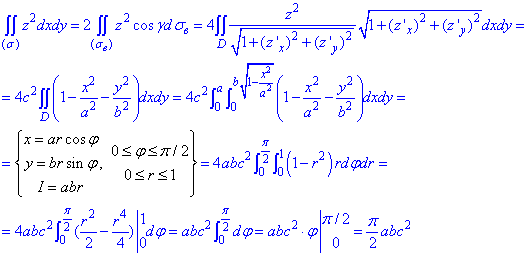
Всі перетворення дають змогу без обчислення важких інтегралів знайти компактну відповідь.
 – зовнішня частина еліпсоїда
– зовнішня частина еліпсоїда 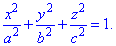
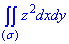
Розв'язання: Побудуємо еліпсоїд та його проекцію в декартову пощину:
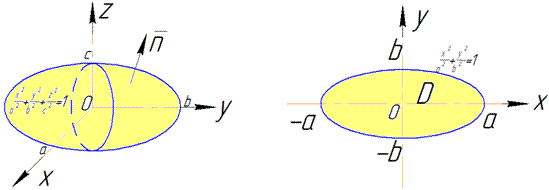
Проекція площини на Oxy обмежена наступним чином
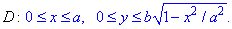
(Взяли чверть області).Далі виражаємо поверхню як функцію z(x,y)
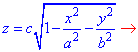
z^2=(1-x^2/a^2-y^2/b^2)*c^2та знаходимо диференціал поверхні за формулою
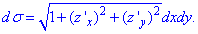
Цей інтеграл будемо обчислювати для верхньої половини еліпсоїда, оскільки для нижньої значення поверхневого інтеграла буде таким же. Таким чином, результат помножимо на 2.
Обчислимо направляючі косинуси заданої поверхні:
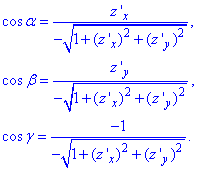
Перед радикалами поставимо знак « – », оскільки нормаль
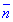 зовнішня утворює з віссю Oz гострий кут. Отже зводимо поверхневий інтеграл до повторного, далі робимо заміну змінних та знаходимо якобіан переходу.
зовнішня утворює з віссю Oz гострий кут. Отже зводимо поверхневий інтеграл до повторного, далі робимо заміну змінних та знаходимо якобіан переходу.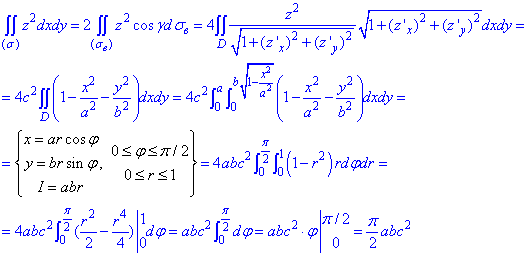
Всі перетворення дають змогу без обчислення важких інтегралів знайти компактну відповідь.
ЗАВДАННЯ 6.9 Обчислити поверхневий інтеграл int((y-z)*dy*dz,ds) по поверхні сігма, де сігма – зовнішня сторона конічної поверхні x^2+y^2=z^2 (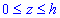 ).
).
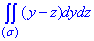
Розв'язання: Побудуємо конус, який обмежений зверху: x^2+y^2=z^2 (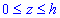 ).
).
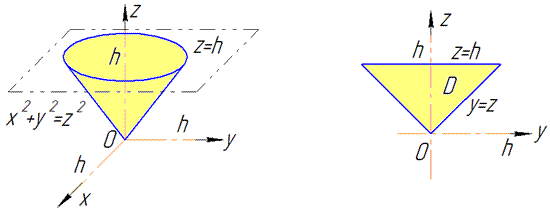
Його проекція в площину Oyz дає рівнобедрений трикутник, обмежений лініями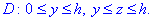
При розстановці меж врахували парність функцій, тому результат потрібно буде помножимо на 2.
Знаходимо поверхневий інтеграл ІІ роду:
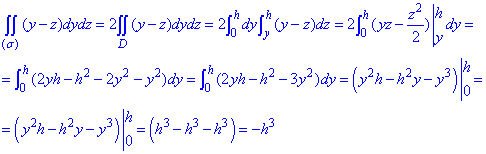
Проінтегрувати наведені функції під силу кожному студенту.
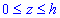 ).
).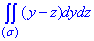
Розв'язання: Побудуємо конус, який обмежений зверху: x^2+y^2=z^2 (
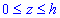 ).
).
Його проекція в площину Oyz дає рівнобедрений трикутник, обмежений лініями
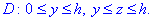
При розстановці меж врахували парність функцій, тому результат потрібно буде помножимо на 2.
Знаходимо поверхневий інтеграл ІІ роду:
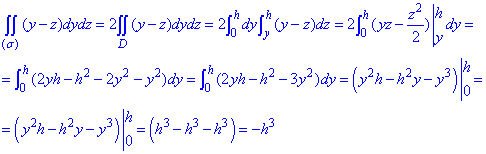
Проінтегрувати наведені функції під силу кожному студенту.
ЗАВДАННЯ 6.13 Обчислити поверхневий інтеграл int(x*dx*dz,ds) по поверхні сігма, де сігма – зовнішня сторона трикутника, утвореного перетином площини x-y+z=1 з координатними осями.
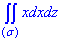
Розв'язання: Побудуємо просторовий трикутник x-y+z=1 та його проекцію.
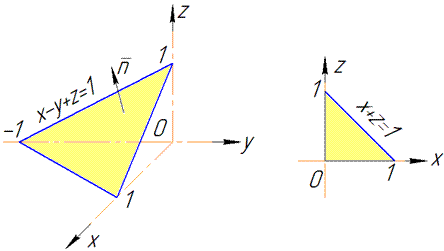
Проектувати завжди слід в ту площину Oxz, по якій йде інтегрування
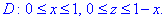
Обчислюмо поверхневий інтеграл ІІ роду:
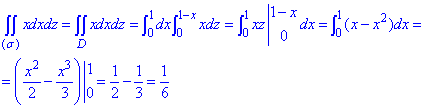
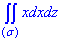
Розв'язання: Побудуємо просторовий трикутник x-y+z=1 та його проекцію.

Проектувати завжди слід в ту площину Oxz, по якій йде інтегрування
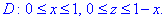
Обчислюмо поверхневий інтеграл ІІ роду:
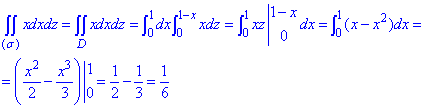
.
ЗАВДАННЯ 6.15 Обчислити поверхневий інтеграл int(yz*dy*dz,ds) по поверхні сігма – зовнішня сторона трикутника, утвореного перетином площини x+y+z=4 з координатними осями.

Розв'язання: Побудуємо площину сігма: x+y+z=4.
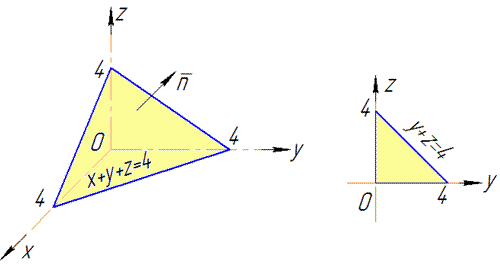
Бачимо, що проекція трикутника в Oyz має такі межі
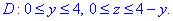
Поверхневий інтеграл ІІ роду зводимо до повторного та обчислюємо
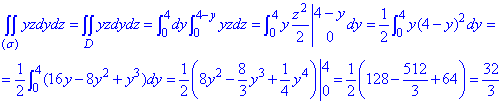
Брати подібні інтеграли не складно, вся проблема зводиться до правильної побудови поверхні та коректного розставлення меж. Інтегрувати не важко, оскільки, як правило, задані найпростіші функції.

Розв'язання: Побудуємо площину сігма: x+y+z=4.

Бачимо, що проекція трикутника в Oyz має такі межі
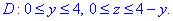
Поверхневий інтеграл ІІ роду зводимо до повторного та обчислюємо
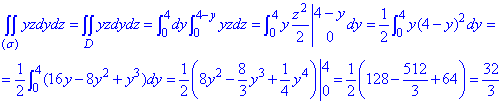
Брати подібні інтеграли не складно, вся проблема зводиться до правильної побудови поверхні та коректного розставлення меж. Інтегрувати не важко, оскільки, як правило, задані найпростіші функції.
ЗАВДАННЯ 6.16 Обчислити поверхневий інтеграл int(xz*dx*dz,ds) по поверхні сігма– зовнішня сторона трикутника, утвореного перетином площини x+y+z=3 з координатними осями.
Розв'язання: Побудуємо просторовий трикутник: x+y+z=3.
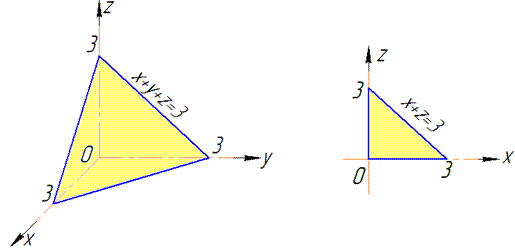
Задана площина проектується на область D в Oxz наступним чином
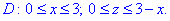
Маючи межі зводимо поверхневий інтеграл ІІ роду до повторного
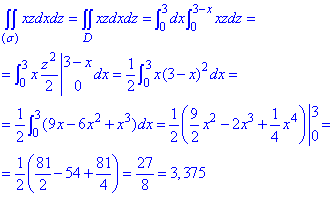
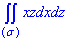
Розв'язання: Побудуємо просторовий трикутник: x+y+z=3.
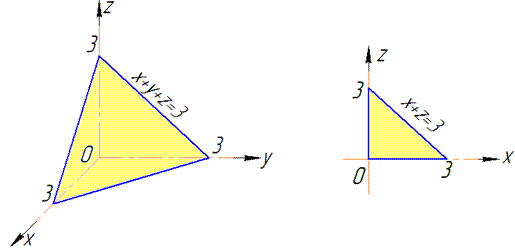
Задана площина проектується на область D в Oxz наступним чином
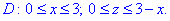
Маючи межі зводимо поверхневий інтеграл ІІ роду до повторного
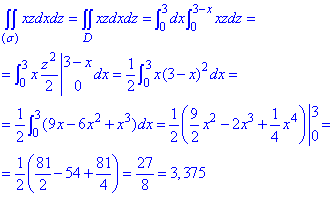
ЗАВДАННЯ 6.17 Обчислити поверхневий інтеграл int(yz*dy*dz,ds) по поверхні сігма – зовнішня сторона трикутника, утвореного перетином площини x+y+z=4 з координатними осями.

Розв'язання: Виконуємо побудову площини: x+y+z=4.

Проекція на площину Oyz обмежена трикутником
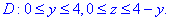
Поверхневий інтеграл ІІ роду знаходимо за формулою
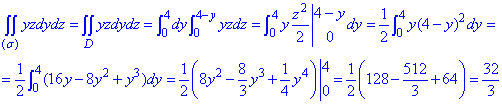

Розв'язання: Виконуємо побудову площини: x+y+z=4.

Проекція на площину Oyz обмежена трикутником
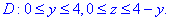
Поверхневий інтеграл ІІ роду знаходимо за формулою
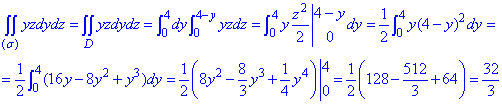
ЗАВДАННЯ 6.23 Обчислити поверхневий інтеграл int((x+z)*dy*dz,ds) по поверхні 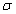 , де
, де 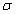 – зовнішня сторона піраміди, обмеженої площинами x=0, y=0, z=0, x+y+z=1.
– зовнішня сторона піраміди, обмеженої площинами x=0, y=0, z=0, x+y+z=1.
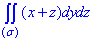
Розв'язання: Виконуємо рисунок до задачі
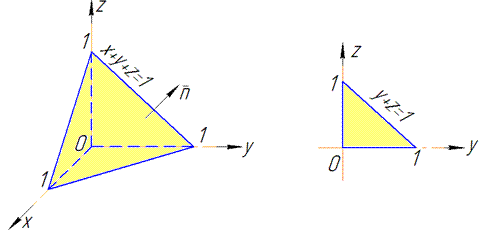
Пплощина проектується трикутником в Oyz
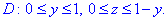
Поверхневий інтеграл ІІ роду обчислюємо з врахуванням рівняння поверхні x=1-y-z.
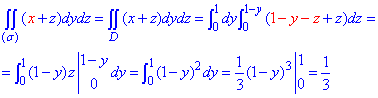
Обчислення самі по собі не важкі, тому на практичних та екзаменах ця тема не має створювати Вам труднощів.
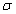 , де
, де 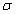 – зовнішня сторона піраміди, обмеженої площинами x=0, y=0, z=0, x+y+z=1.
– зовнішня сторона піраміди, обмеженої площинами x=0, y=0, z=0, x+y+z=1.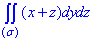
Розв'язання: Виконуємо рисунок до задачі

Пплощина проектується трикутником в Oyz
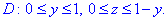
Поверхневий інтеграл ІІ роду обчислюємо з врахуванням рівняння поверхні x=1-y-z.
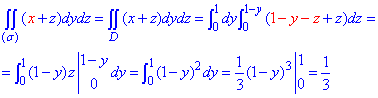
Обчислення самі по собі не важкі, тому на практичних та екзаменах ця тема не має створювати Вам труднощів.
Немає коментарів:
Дописати коментар