Приклад 8. Інтеграл знаходимо за правилом інтегрування частинами int(udv)=u*v-int(vdu). Тут головне правильно вибрати функції під правило. (Для себе запам'ятайте, що за dv вибирають періодичні функції, та такі які при диференціюванні з точністю до множника дають самі себе – експонента). В цьому інтегралі потрібно синус внести під диференціал
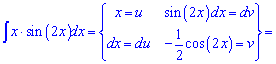
Подальше інтегрування достатньо просте і на деталях зупинятися не будемо.
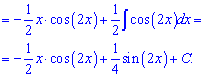
Приклад 9. Знову потрібно застосовувати правило інтегрування частинами udv. Тут маємо добуток періодичної функції на експоненту, тому що вносити під диференціал вибирати Вам. Можна як експоненту, так і косинус (отримаємо рекурентну формулу).
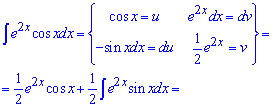
Застосовуємо внесення під диференціал повторно
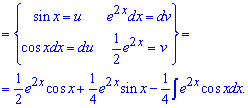
Прийшли до рекурентної формули. Якщо записати інтеграл, який шукали та результат обчислень то отримаємо два подібні доданки
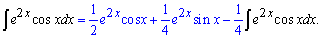
Групуємо їх та знаходимо шуканий інтеграл
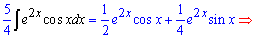
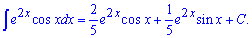
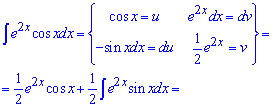
Застосовуємо внесення під диференціал повторно
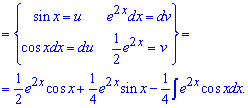
Прийшли до рекурентної формули. Якщо записати інтеграл, який шукали та результат обчислень то отримаємо два подібні доданки
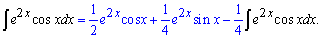
Групуємо їх та знаходимо шуканий інтеграл
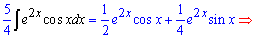
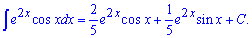
Приклад 10. Маємо готовий запис інтегралу під правило udv. Знаходимо du та виконуємо інтегрування
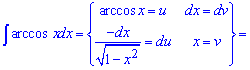
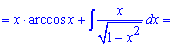
Зводимо інтеграл під табличну формулу та обчислюємо його
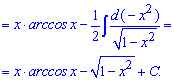
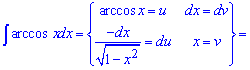
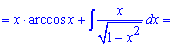
Зводимо інтеграл під табличну формулу та обчислюємо його
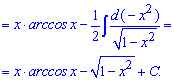
Приклад 11. Позначимо cos(ln(x))=u і знайдемо du для формули інтегрування, внесенням під диференціал
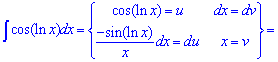
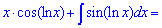
До інтегралу повторно застосовуємо правило
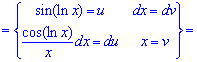

Прийшли до рекурентної формули
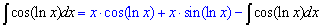
з якої і обчислюємо невідомий інтеграл
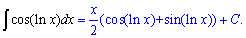
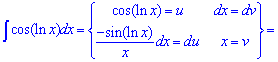
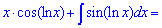
До інтегралу повторно застосовуємо правило
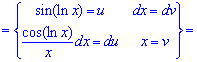

Прийшли до рекурентної формули
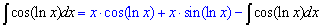
з якої і обчислюємо невідомий інтеграл
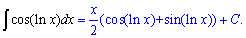
Приклад 12. Для знаходження інтегралу виділимо в знаменнику повний квадрат. Далі застосовуємо табличний інтеграл
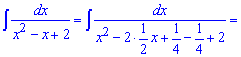
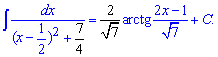
Добре запам'ятайте порядок чергування множників. Одиниця розділена на корінь з вільного члена фігурує перед арктангенсом, також цей множник присутній в арктангенсі перед змінною.
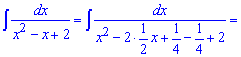
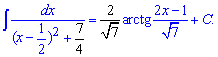
Добре запам'ятайте порядок чергування множників. Одиниця розділена на корінь з вільного члена фігурує перед арктангенсом, також цей множник присутній в арктангенсі перед змінною.
Приклад 13. Подібний інтеграл, тільки в знаменнику вже маємо корінь з квадратичної залежності. Виділяємо повний квадрат та зводимо під формули інтегрування
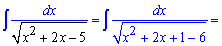
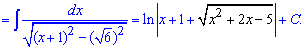
Ось такі бувають приклади на контрольній чи тестах. Добре запам'ятайте основні схеми інтегрування.
Як тільки Ви вивчите наведені схеми та методики зведення інтегралів під те чи інше правило, навчитеся бачити в прикладах табличні інтеграли та перетворення, які в кілька кроків дозволять Вам знайти інтеграл – то будь-яка контрольна робота, чи "зрізи" для Вас не будуть перешкодою в навчанні. Для цього потрібно розв'язати з десяток різних інтегралів до кожного з наведених прикладів. Всі решта після цього будуть для Вас подібними, а схема їх обчислень очевидною і зрозумілою для Вас. Якщо в навчанні зустрічаються складні інтеграли, або ж маєте сумніви у власних силах пам'ятайте – ми завжди готові надати допомогу. Як на контрольних так і на тестах, ця пропозиція актуальна не тільки для студентів стаціонарної форми навчання, а й для заочників та школярів. В 11 класі в навчанні з недавніх часів школярам також доводиться мати справу з інтегралами.
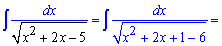
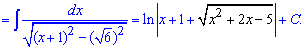
Ось такі бувають приклади на контрольній чи тестах. Добре запам'ятайте основні схеми інтегрування.
Як тільки Ви вивчите наведені схеми та методики зведення інтегралів під те чи інше правило, навчитеся бачити в прикладах табличні інтеграли та перетворення, які в кілька кроків дозволять Вам знайти інтеграл – то будь-яка контрольна робота, чи "зрізи" для Вас не будуть перешкодою в навчанні. Для цього потрібно розв'язати з десяток різних інтегралів до кожного з наведених прикладів. Всі решта після цього будуть для Вас подібними, а схема їх обчислень очевидною і зрозумілою для Вас. Якщо в навчанні зустрічаються складні інтеграли, або ж маєте сумніви у власних силах пам'ятайте – ми завжди готові надати допомогу. Як на контрольних так і на тестах, ця пропозиція актуальна не тільки для студентів стаціонарної форми навчання, а й для заочників та школярів. В 11 класі в навчанні з недавніх часів школярам також доводиться мати справу з інтегралами.
Немає коментарів:
Дописати коментар