Дана стаття вчить розв'язувати інтеграли виду
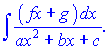
Для знаходження таких інтегралів потрібно перетворити їх до відомих формул інтегрування, що в сво чергупотебує спочатку виділити повний квадрат із квадратного рівняння.
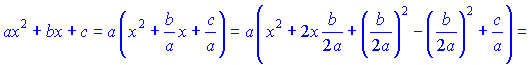
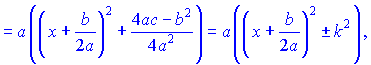
де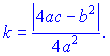
Подальше інтегрування зводиться до відшукання табличних інтегралів. Розглянемо конкретні приклади, для закріплення даного матеріалу.
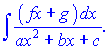
Для знаходження таких інтегралів потрібно перетворити їх до відомих формул інтегрування, що в сво чергупотебує спочатку виділити повний квадрат із квадратного рівняння.
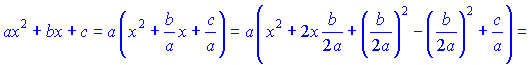
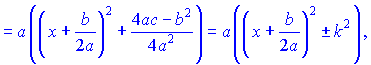
де
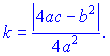
Подальше інтегрування зводиться до відшукання табличних інтегралів. Розглянемо конкретні приклади, для закріплення даного матеріалу.
Приклад 1. Обчислити інтеграли
а) 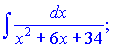
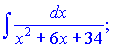
Розв'язок. Виділимо повний квадрат з рівняння
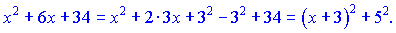
Наш інтеграл набуде вигляду
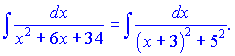
Для зведення до табличного вигляду виконаємо заміну змінних
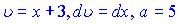
і проінтегруємо
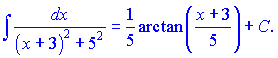
Неозначений інтегра рівний атангенсу частки коренів з доданків знаменника.
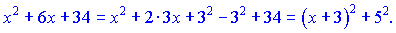
Наш інтеграл набуде вигляду
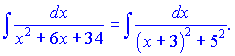
Для зведення до табличного вигляду виконаємо заміну змінних
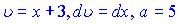
і проінтегруємо
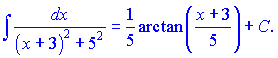
Неозначений інтегра рівний атангенсу частки коренів з доданків знаменника.
б) 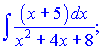
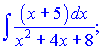
Розв'язок. Даний тип інтегралу складніший від попереднього тим, що в чисельнику маємо функцію від x Такі інтеграли знаходять наступним чином. Спочатку робимо заміну змінних
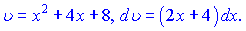
Для одержання в чисельнику виразу порядку (2x+4)dx помножимо і поділимо наш чисельник на 2. Отримаємо
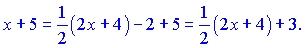
Якщо б в чисельнику замість x+5 мали x+2, то інтегрування можна звести до відшукання одного інтегралу. Проте такий варіант вибраний спеціально, щоб навчити Вас більше. З такою заміною розбиваємо інтеграл на два доданки
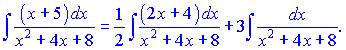
Заміну ми робили для того, щоб легко було звести перший доданок до табличного логарифма
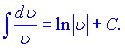
У нашому випадку один інтеграл рівний логарифму квадратичної функції
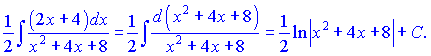
Другий доданок зводиться за схемою, наведеною в попередньому прикладі. Для цього в знаменнику виділяємо повний квадрат
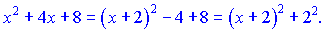
Тоді інтеграл зводимо під арктангенс
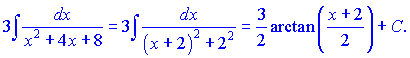
Остаточно, шуканий інтеграл рівний сумі двох знайдених
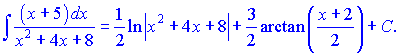
Схема зведення добре працює, коли в знаменнику легко виділяється повний квадрат, в інших випадках доводиться мати справу з коренями.
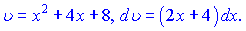
Для одержання в чисельнику виразу порядку (2x+4)dx помножимо і поділимо наш чисельник на 2. Отримаємо
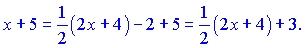
Якщо б в чисельнику замість x+5 мали x+2, то інтегрування можна звести до відшукання одного інтегралу. Проте такий варіант вибраний спеціально, щоб навчити Вас більше. З такою заміною розбиваємо інтеграл на два доданки
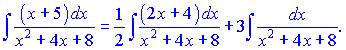
Заміну ми робили для того, щоб легко було звести перший доданок до табличного логарифма
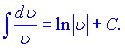
У нашому випадку один інтеграл рівний логарифму квадратичної функції
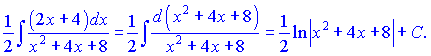
Другий доданок зводиться за схемою, наведеною в попередньому прикладі. Для цього в знаменнику виділяємо повний квадрат
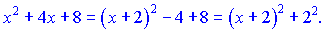
Тоді інтеграл зводимо під арктангенс
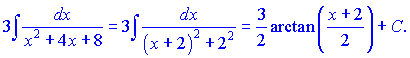
Остаточно, шуканий інтеграл рівний сумі двох знайдених
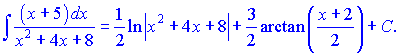
Схема зведення добре працює, коли в знаменнику легко виділяється повний квадрат, в інших випадках доводиться мати справу з коренями.
Також зустрічаються приклади коли в чисельнику зустрічаються функції f(x) вищих порядків – квадратні рівняння, кубічні і старші. В таких випадках, їх ділимо на знаменник і зводимо до розглядуваного вигляду.
в)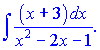
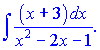
Розв'язок. Робимо заміну змінних
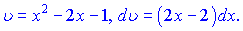
Щоб одержати в чисельнику вираз, який містить(2x-2)dx помножимо і поділимо наш чисельник на 2:
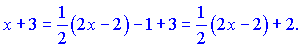
Заданий інтеграл запишемо у вигляді суми двох доданків
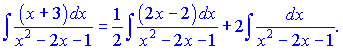
Перший доданок дасть логарифм квадратичної функції
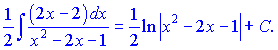
Для знаходження другого виділяємо в знаменнику повний квадрат
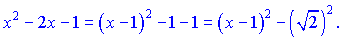
Застосовуючи табличну формулу до другого доданку, отримаємо логарифм частки функцій
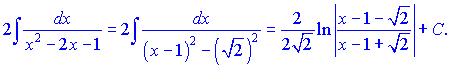
Сумуючи доданки, матимемо значення неозначеного інтегралу
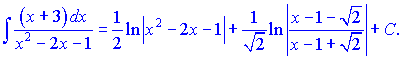
Розглянуті три приклади описують найпоширеніші завдання даної теми. Якщо Вам зустрінуться складніші інтеграли спробуйте знайти розв'язок самостійно, якщо не зможете розв'язати звертайтеся до нас.
Практикуйте і подібні інтеграли не будуть для Вас перешкодою в навчанні.
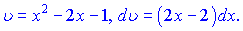
Щоб одержати в чисельнику вираз, який містить(2x-2)dx помножимо і поділимо наш чисельник на 2:
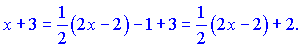
Заданий інтеграл запишемо у вигляді суми двох доданків
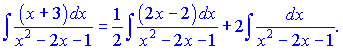
Перший доданок дасть логарифм квадратичної функції
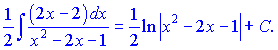
Для знаходження другого виділяємо в знаменнику повний квадрат
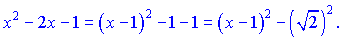
Застосовуючи табличну формулу до другого доданку, отримаємо логарифм частки функцій
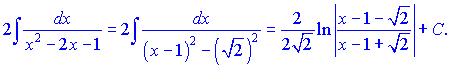
Сумуючи доданки, матимемо значення неозначеного інтегралу
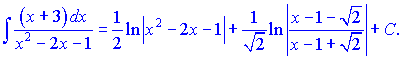
Розглянуті три приклади описують найпоширеніші завдання даної теми. Якщо Вам зустрінуться складніші інтеграли спробуйте знайти розв'язок самостійно, якщо не зможете розв'язати звертайтеся до нас.
Практикуйте і подібні інтеграли не будуть для Вас перешкодою в навчанні.
Немає коментарів:
Дописати коментар