Формула рівняння регресії
Продовжуємо аналізувати відповіді до індивідуальних завдань з теорії ймовірностей. З цієї статті Ви навчитеся складати (будувати) рівняння прямої регресії Y на X. Такі завдання поширені у навчанні з теорії ймовірностей для студентів економічного факультету та статистів. Наведені розв'язки взято з програми для економістів ЛНУ ім. І.Франка. ВУЗи Києва, Одеси, Харкова та інших міст України мають подібну систему навчання, тому багато корисного для себе повинен узяти кожен студент. Завдання іншої тематики поєднані між собою посиланнями у кінці статті, тож шукайте, що Вас цікавить.
Індивідуальне завдання 1
Варіант 11
Завдання 1. Зв'язок між ознаками Х і Y генеральної сукупності задається таблицею:

Записати вибіркове рівняння прямої регресії Y на X.
Індивідуальне завдання 1
Варіант 11
Завдання 1. Зв'язок між ознаками Х і Y генеральної сукупності задається таблицею:

Записати вибіркове рівняння прямої регресії Y на X.
Розв'язання: Обчислюємо середні арифметичні значення множини Х та Y
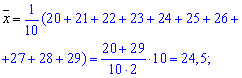
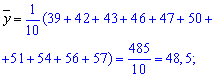
Знаходимо величини, які фігурують в рівнянні регресії коефіцієнтами alpha, beta
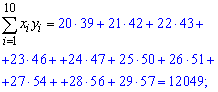
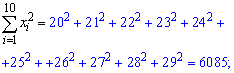
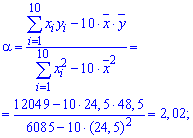
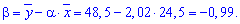
Після обчислень вибіркове рівняння регресії Y на X записуємо формулою
y=2,02*x-0,99.
Щоб підтвердити правильність припущення про лінійність зв' язку між ознаками Х і Y знаходимо вибірковий коефіцієнт кореляції за формулою:
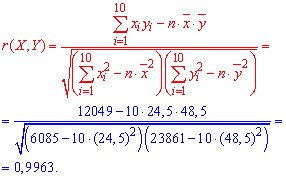
Так як вибірковий коефіцієнт кореляції r(X,Y) є досить близьким до одиниці, то припущення про лінійність зв'язку між X і Y - правильне. Крім цього, коефіцієнт кореляції додатний r>0, тому випадкові величини X і Y збільшуються одночасно.
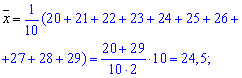
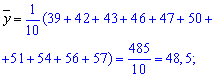
Знаходимо величини, які фігурують в рівнянні регресії коефіцієнтами alpha, beta
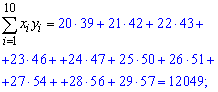
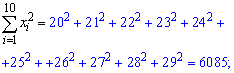
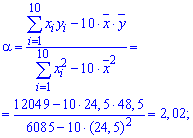
Після обчислень вибіркове рівняння регресії Y на X записуємо формулою
y=2,02*x-0,99.
Щоб підтвердити правильність припущення про лінійність зв' язку між ознаками Х і Y знаходимо вибірковий коефіцієнт кореляції за формулою:
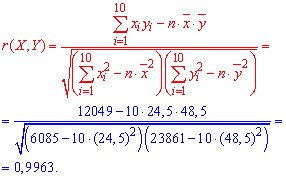
Так як вибірковий коефіцієнт кореляції r(X,Y) є досить близьким до одиниці, то припущення про лінійність зв'язку між X і Y - правильне. Крім цього, коефіцієнт кореляції додатний r>0, тому випадкові величини X і Y збільшуються одночасно.
Варіант 1
Завдання 1. Зв'язок між ознаками Х і Y генеральної сукупності задається таблицею:

Записати вибіркове рівняння прямої регресії Y на X.

Записати вибіркове рівняння прямої регресії Y на X.
Розв'язання: Знаходимо величини, які необхідні для обчислення коефіцієнтів рівняння регресії
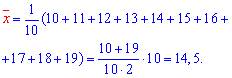
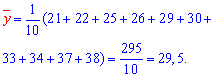
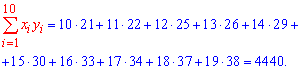
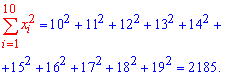
Обчислюємо alpha, beta за формулами
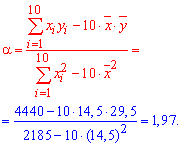
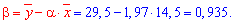
та складаємо рівняння регресії Y на X
y=19,7*x+0,935.
Для того, щоб переконатися, що припущення про лінійність зв' язку між Х і Y є правильним, знаходимо вибірковий коефіцієнт кореляції за формулою:
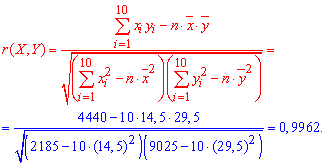
Оскільки знайдений вибірковий коефіцієнт кореляції r(X,Y)=0,9962 є досить близьким до одиниці, то припущення про лінійність зв'язку між X і Y - правильне.
Крім цього коефіцієнт кореляції додатний (r>0), тому і зв'язок між X і Y є додатний, тобто ці випадкові величини збільшуються одночасно.
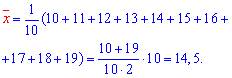
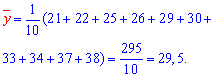
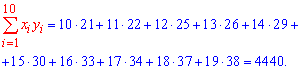
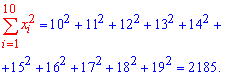
Обчислюємо alpha, beta за формулами
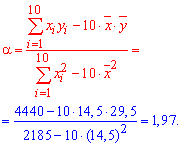
та складаємо рівняння регресії Y на X
y=19,7*x+0,935.
Для того, щоб переконатися, що припущення про лінійність зв' язку між Х і Y є правильним, знаходимо вибірковий коефіцієнт кореляції за формулою:
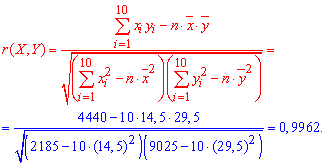
Оскільки знайдений вибірковий коефіцієнт кореляції r(X,Y)=0,9962 є досить близьким до одиниці, то припущення про лінійність зв'язку між X і Y - правильне.
Крім цього коефіцієнт кореляції додатний (r>0), тому і зв'язок між X і Y є додатний, тобто ці випадкові величини збільшуються одночасно.
Варіант-12
Завдання 1. Зв'язок між ознаками Х і Y генеральної сукупності задається таблицею:

Записати вибіркове рівняння прямої регресії Y на X.

Записати вибіркове рівняння прямої регресії Y на X.
Розв'язання: Обчислюємо середні арифметичні значення кожної з вибірок, а також решта складових для побудови рівняння регресії Y на X:
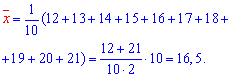
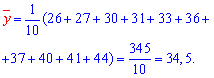
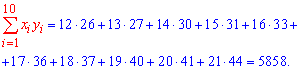
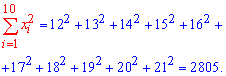
Знаходимо коефіцієнти alpa, beta за формулами
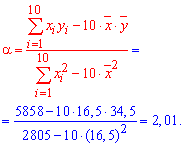
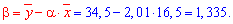
Підставляємо коефіцієнти в рівняння прямої регресії y=2,01*x+1,335.
Знаходимо точкову оцінку для коефіцієнта кореляції за формулою:
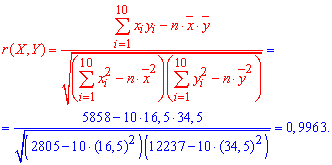
Оскільки вибірковий коефіцієнт кореляції r(X,Y) є досить близьким до одиниці, то припущення про лінійність зв'язку між X і Y - правильне.
Крім цього, r>0, тому зв'язок між X і Y є додатний і ці випадкові величини збільшуються одночасно.
Тепер Ви знаєте, як скласти рівняння прямої регресії Y на X .
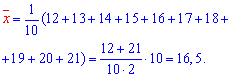
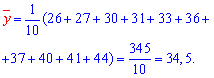
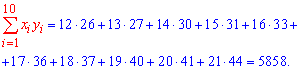
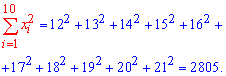
Знаходимо коефіцієнти alpa, beta за формулами
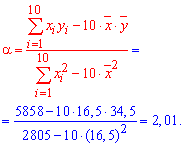
Підставляємо коефіцієнти в рівняння прямої регресії y=2,01*x+1,335.
Знаходимо точкову оцінку для коефіцієнта кореляції за формулою:

Оскільки вибірковий коефіцієнт кореляції r(X,Y) є досить близьким до одиниці, то припущення про лінійність зв'язку між X і Y - правильне.
Крім цього, r>0, тому зв'язок між X і Y є додатний і ці випадкові величини збільшуються одночасно.
Тепер Ви знаєте, як скласти рівняння прямої регресії Y на X .
Немає коментарів:
Дописати коментар