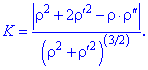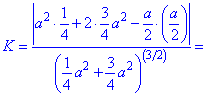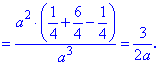Запитання: Чому обернена до лінійної функції являється лінійною функцією?
Відповідь: Графіки двох взаємно обернених функцій мають властивість симетрії відносно прямої у = х. А графіком лінійної функції(бієктивна функція) є пряма лінію. А при симетричному відображені пряма переходить у пряму лінію. А прямі в системі координат можуть бути задані лінійними функціями. Тому дві лінійні функції
f(x)=kx+l,
p(x)=ax+b,
називаються взаємно оберненими, якщо виконується рівність
f(p(x)) = p(f(x)) = х.
Знайти лінійну функцію р(х) таку, що виконується
р(f(х)) = f(p(x))= х,
якщо f(х)= -4х + 3.
Розв’язання:
Спочатку
з’ясуємо, чи дана функція може мати обернену. Якщо припустити, що дана функція
немає оберненої, то повинні існувати такі значення х1= х2, для
яких f(х1)=f( х2). Тоді -4х1+3=-4х2+3 звідки х1 = х2.
Дане протиріччя доводить, що дана функція має обернену.
Розпочнемо конструювати взаємно обернену
функцію. Нехай у=-4х+3. Замінимо х
на у. А потім виразимо у через х.
х = -4у + 3, звідси -4у = х - 3,
остаточно у = -0,25х + 0,75.
Таким чином,
f(х)= -4х + 3 та р(х) = -0,25х +
0,75. Виконаємо перевірку.
р(f(х))= -0,25(-4х + 3) +
0,75 = х - 0,75 + 0,75 = х.
Області визначення та області значення обох
функцій становлять множину дійсних чисел.
Відповідь: р(х) = -0,25х + 0,75.
Запитання: Чому обернена до лінійно-дробової функції являється лінійно-дробовою функцією?
Відповідь: Графіки двох взаємно обернених функцій мають властивість симетрії відносно прямої у = х. А графіком лінійно-дробової функції є рівностороння гіпербола(це бієктивна функція), з асимптотами паралельними осям координат. А при симетричному відображені графік гіперболи, переходить у гіперболу з тими самими відстанями між відповідними точками. А гіперболи в системі координат можуть бути задані лінійно-дробовими функціями. Тому дві лінійно-дробові функції
f(x)=(kx+l)/(nx+m),
p(x)=(ax+b)/(cx+d),
називаються взаємно оберненими, якщо виконується рівність
f(p(x)) = p(f(x)) = х.
Знайти лінійно-дробову функцію р(х) таку, що виконується
р(f(х)) = f(p(x)) = х,
якщо f(х)= (2х + 1)/(3х + 2).
Розв’язання:
Спочатку з’ясуємо, чи дана функція може мати обернену. Якщо припустити, що дана функція немає оберненої, то повинні існувати такі значення х1=х2, для яких f(х1)=f( х2). Тоді (2х1 + 1)/(3х1 + 2) = (2х2 + 1)/(3х2 + 2) звідки х1 = х2. Дане протиріччя доводить, що дана функція має обернену.
Розпочнемо конструювати взаємно обернену функцію. Нехай f(х)=у = (2х + 1)/(3х + 2). Замінимо х на у. А потім виразимо у через х. І отримаємо у =
,
остаточно у = р(х) =
Таким чином,
f(х)= (2х + 1)/(3х + 2) та (-х + 1)/(3х - 2)..
Виконаємо перевірку виразу
Області визначення та області значення обох функцій взаємно обмінюються.
Відповідь: р(х) =
Застосування поняття групи
для
знаходження розв’язку
функціонального рівняння.
Означення групи функцій.
Довільна множина G функцій, визначених на
деякій множині М називається групою
відносно операції композиції, якщо вона володіє такими властивостями:
1. Для будь-яких
двох функцій з множини G Їх композиція також належить G.
2. Функція f(х)=х теж належить множині G.
3. Для будь-якої
функції f(х) з множини G існує обернена функція f -1 (х), яка належить множині G.
Наведемо
приклади таких груп функцій:
а) Множина лінійних функцій pn(х) = ах+b,
де а - дійсне число, крім 0, b - дійсне число;
б) p1(х)=х, p2(х)=, 1/(1-x) p3(х)=(x-1)/x;
в) p1= x, p2= a-x;
г) p1= x, p2= a/x;
д) p1= x, p2= a/x; p3= -x, p4=
-a/x;
е) p1= x, p2=
1/x; p3= -x, p4= -1/x; p5= (x-1)/(x+1), p6=
(1+x)/(x-1); p7= (1-x)/(x+1);, p8= (1+x)/(1-x);
є) p1= x, p2=
a2/x; p3= a-x, p4=
ax/(x-a); p5= (ax-a2)/x,
p6= a2/(a-x);
У функціональному
співвідношенні чи рівнянні виду
К1f(p1)+ К2f(p2)+ К3f(p3)+....+ Кnf(pn) =М (*)
вирази, які стоять під
знаком невідомої функції f(х) являються елементами групи G, яка
складається із n функцій:
причому
коефіцієнти К1, К2,....., Кn, та М – довільні функції, що задовольняють додатковим
обмеженням на рівняння.
Припустимо, що
функціональне рівняння (*) має розв’язок. Виконаємо
послідовні
Композиції, тобто виконаємо підстановку х = p2 (x)
p1 p2, p2
p2, p2 p2 , p3
p2 , p3 p2,
........., pn
p2,
........., pn p2.
p2.
Остання
послідовність складається з елементів групи. Продовжимо виконувати послідовні
підстановки,
х p3 (x), х
p3 (x), х p4 (x), х
p4 (x), х p5(x)
p5(x)
щоб
отримати систему із n лінійних
функціональних рівнянь.
Якщо
вдається розв’язати цю систем, то слід перевірити розв’язок, чи задовольняє він
рівняння(*).
https://www.youtube.com/watch?v=bSEwOnzPrpU - урок тиврівського учителя математики Володимира Сидорука "СПОСІБ підстановки для функціональних рівнянь"
Відкритий урок: "Функціональні рівняння". Олександр Храбров
Знаходження
розв’язку функціонального рівняння,
які зводяться до квадратного виду.
Функціональне рівняння виду
а(x) f2 (x) + b(x) f (x) + с(x) = 0, (8.1 )
де а(х), b(х), с(х), –
ненульові відомі функції дійсного аргументу х,
f – невідома
функція дійсного аргументу
формально
може мати розв’язок, якщо D = b2-4ас>=0. Його можна знайти за стандартною
схемою розв’язання квадратних рівнянь.
Приклад 1. Знайти розв’язок f: R відображає в R функціонального
рівняння та перевірити його, якщо
f2 (x) - (cos x) f (x) – 0,25 – 0,5 cos x = 0, (8.2
)
Розв’язання: Розпочнемо конструювати
дискримінант , щоб впевнитися ,чи
має рівняння розв’язки.
D = в2-4ас = (-cos x )2 – 4(– 0,25 – 0,5 cos x)=(1+ cos x)2 - невідємний
За формулою розв’язків квадратного рівняння
відшукуємо
f 1 (x)=-(cosx-1-cosx)/2
= 0,5
f 2(x)= (cosx+1+cosx)/2 =cosx+0,5
Таким чином, два розв’язки
f 1 (x)=
-0,5,
f 2(x)= cos x + 0.5
перевіряємо для даного рівняння. (8.2 ).
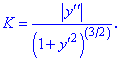
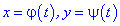 то кривина визначається залежністю
то кривина визначається залежністю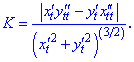
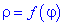 обчислюється за формулою
обчислюється за формулою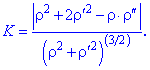
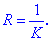
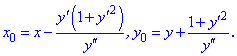
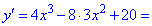
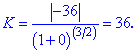
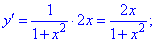
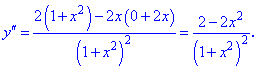
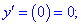
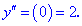
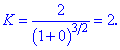
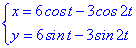 в точці
в точці 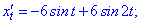
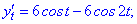
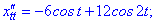
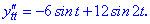
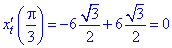
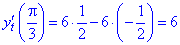
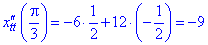
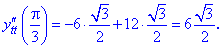
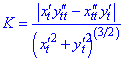
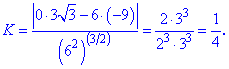
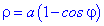 при
при 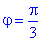 .
.